Moeller diagram: what it is, how it is used in Chemistry, and examples
Chemistry can be especially complicated, so any tool that facilitates learning for those who are introduced to it is welcome.
One of the most popular methods of becoming familiar with Madelung's rule and the electron configuration of atoms is the Moeller diagram, a graphical mnemonic rule that makes it much easier to see in which orbitals the electrons.
Next we are going to discover what the Moeller diagram consists of, how it relates to Madelung's rule, how it is applied by means of a few solved examples, and which chemical elements do not obey this strategy.
- Related article: "The 5 types of chemical bonds: this is how matter is made up"
What is the Moeller diagram?
The Moeller diagram, also known as the rain method or the rule of diagonals, is a graphic and mnemonic method for learning Madelung's rule, a technique for knowing and writing the electronic configuration of chemical elements.
This diagram is characterized by drawing diagonals through the columns of the orbitals, from top to bottom from right to left. Through the Moeller diagram, an order is defined in the filling of the orbitals, which will be defined by three quantum numbers: n, l and ml.
The Moeller diagram works according to the following:

Each column corresponds to a different orbital through which the electrons of an atom circulate, subatomic particles that have a negative charge. The orbitals in question are: s, p, d and f, each with a specific space to house electrons and, therefore, different energy levels.
If we draw the diagonals or arrows in the aforementioned sense, we have that the first orbital is 1s. The second arrow begins with the 2s orbital. The third arrow crosses 2p and 3s. The fourth diagonal is 3p and 4s. The fifth diagonal is 3d, 4p and 5s and so on. The Moeller diagram is an introductory technique for those beginning to study the electronic configurations of the elements of the periodic table in chemistry.
- You may be interested in: "The 6 main branches of the natural sciences"
Madelung's rule
Since the Moeller diagram is the graphical representation of Madelung's rule (also known as Klechkovsky's rule in some countries) we must first know what it is about. According to this rule, the filling of the orbitals of an atom must obey the following two rules:
Madelung's first rule
The orbitals with the lowest values of n + l are filled first, with n being the principal quantum number, and l being the orbital angular momentum..
For example, the 3d orbital corresponds to n = 3 and l = 2. Therefore, n + l = 3 + 2 = 5. Instead, the 4s orbital corresponds to n = 4 and l = 0, therefore n + l = 4 + 0 = 4. From this it is established that the electrons fill the 4s orbital first before the 3d one, because 4s = 4 while 3d = 5.
- Related article: "The 11 types of chemical reactions"
Madelung's second rule
If two orbitals have the same value of n + l, the electrons will first occupy the one with the lower value of n.
For example, the 3d orbital has a value of n + l = 5, identical to that of the 4p orbital (4 + 1 = 5) but, since the 3d orbital has the lowest value for n, it will be filled first than the 4p orbital.
From all these observations and rules, the following order can be reached in the filling of the atomic orbitals: 1s 2s 2p 3s 3p 4s 3d 4p. Although this order is fixed, remembering it by heart is complicated, which is why there is a Moeller diagram that graphically represents its order.
- You may be interested in: "The 9 postulates of Dalton's atomic theory"
Steps to follow when using the Moeller diagram
As we have commented in the previous section, Madelung's rule uses the formula n + l to establish what orbitals are filled before and from that determine what is the electronic configuration of an element determined. However, the Moeller diagram already represents this graphically and easily, so it is enough to follow the columns of the same diagram and draw diagonals to find out in what order the orbitals of each element.
To discover the electronic configuration of an atom and in which orbitals its electrons are located, we must first know its atomic number Z. The number Z corresponds to the number of electrons in an atom, as long as this atom is neutral, or what is the same, that it is not an ion, neither positive (cation) nor negative (anion).
Thus, knowing Z for a neutral atom, we already know how many electrons a neutral atom of that element usually has. With this in mind, we will begin to draw the diagonals on the Moeller diagram. We must take into account that each type of orbital has a different capacity to house electrons, which are:
- s = 2 electrons
- p = 6 electrons
- d = 10 electrons
- f = 14 electrons
It stops at the orbital where the last electron given by Z has been occupied.
Moeller diagram examples
To better understand how the Moeller diagram works, below we are going to see a few practical examples of setting the electron configuration of different elements.
Beryllium
To establish the electronic configuration of a neutral beryllium (Be) atom, what we must first do is look for it in the periodic table, an alkaline earth that is located in the second column and second row of the table. Its atomic number is 4, therefore Z = 4 and it also has 4 electrons.
Taking all this into account, we are going to use the Moeller diagram to see how the 4 electrons of this element are located. We start by making diagonals in the aforementioned sense, from top to bottom and from right to left.
When we are filling orbitals, It is recommended to put the number of electrons found in each of them as a superscript. Since 1s is the first orbital and it occupies two electrons, we will write it:

Since we still have free electrons, we continue to fill in orbitals. The next is the 2s orbital and, as with 1s, it occupies 2 electrons, therefore 2s2. As we already have all the electrons well located in the orbitals of the neutral atom of Be we can say that the electronic configuration of this element is:

We make sure that we have done well by adding the superscripts: 2 + 2 = 4
- You may be interested in: "Molecular kinetic theory: the 3 states of matter"
Match
The element phosphorus (P) is a nonmetal found in the third row and column 16 of the periodic table, with Z = 15, therefore it has 15 electrons in total that must occupy the orbitals.
Having seen the previous example, we can move forward a bit and locate 4 of its electrons in the same orbitals that beryllium has for its 4 electrons, missing 9 electrons plus.

After the 2s orbital, the next diagonal enters the 2p orbital and ends at the 3s orbital. The 2p orbital can occupy 6 electrons, and in the case of 3s only 2. Thus, we would have:
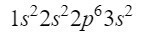
At the moment we have 12 electrons well located, but we still have 3 more to go. We make another diagonal and this time we enter through the 3p orbital according to the Moeller diagram, an orbital that has space for 6 electrons, but since we only have 3 electrons left, this orbital will not be completely occupied, putting 3 as a superscript. Thus, to end phosphorus, its electronic configuration is as follows:

We make sure that we have done well by adding the superscripts: 2 + 2 + 6 + 2 + 3 = 15
Zirconium
The element zirconium (Zr) is a transition metal found in column 4 and row 5 and has a Z = 40. Shortening the path taking advantage of the previous example, we can locate the first 18 electrons.
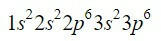
After the 3p orbital, the next ones to fill up, guiding us with the Moeller diagram, are the 4s, 3d, 4p and 5s orbitals, with capacity for 2, 10, 6 and 2 electrons respectively.

Completing the first nine orbitals in the diagram adds a total of 20 electrons, leaving the 2 remaining electrons that are housed in the next orbital, the 4d. Thus, the electron configuration of the neutral element zirconium is:
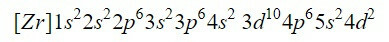
We make sure we have done it right by adding the superscripts: 2 + 2 + 6 + 2 + 6 + 2 + 10 + 6 + 2 + 2 = 40
Oxygen
Here we see a slightly more complicated example that is oxygen (O). This gas is found in column 16 and row 2 of the periodic table, it is a nonmetal and has an atomic number of 8.
So far, looking at the other examples, we would think that its Z = 8, however it is not so simple because this gas is of a special nature, almost always being in the form of an ion with a charge of -2.
This means that, although a neutral oxygen atom does have 8 electrons as indicated by its atomic number, it does It is true that in nature it has more, in its case 10 (8 electrons + 2 electrons or, if you prefer, -8 charge electric -2).
So, in this case, the number of electrons that we have to place in the orbitals is not 8 but 10 electrons, as if we were locating the electrons of the chemical element neon that does have Z = 10.
Understanding this, we only have to do the same thing that we have been doing in the previous cases only taking into account that we are working with an ion (anion):
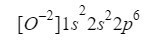
We make sure that we have done well by adding the superscripts: 2 + 2 + 6 = 10
Calcium
Something similar to oxygen happens to calcium (Ca), only in this case we are talking about a cation, that is, an ion with a positive charge.
This element is found in column 2 row 4 of the periodic table with an atomic number of 20, however, in the Nature is usually presented in the form of an ion with a positive charge +2, which means that its electronic charge is 18 (- 20 + 2 = 18; 20 electrons - 2 electrons = 18 electrons).
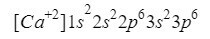
We make sure that we have done well by adding the superscripts: 2 + 2 + 6 + 2 + 6 = 18
Exceptions to the Moeller diagram and Madelung's rule
Although the Moeller diagram is very useful to understand Madelung's rule and to know how the electrons of the different chemical elements are located, the truth is that it is not infallible. There are certain substances whose composition does not obey what we have explained.
Their electron configurations differ experimentally from those predicted by Madelung's rule for quantum reasons.. Among these elements that do not follow the standards we have: chromium (Cr, Z = 24), copper (Cu, Z = 29), silver (Ag, Z = 47), rhodium (Rh, Z = 45), cerium (Ce, Z = 58), niobium (Nb; Z = 41), among others.
Exceptions are very frequent when filling the d and f orbitals. For example, in the case of chromium, which should have a valence configuration ending in 4s ^ 2 3d ^ 4 according to the Moeller diagram and Madelung's rule, it actually has a valence configuration of 4s ^ 1 3d ^ 5. Another strange example is that of silver, which instead of having 5s ^ 2 4d ^ 9 as the last one, has 5s ^ 1 4d ^ 10.

