How to get the AREA of a hexagon
From a Teacher we bring you a lesson in which you are going to learn how to find the area of a hexagon, a basic aspect for the study of geometry and, in general, of mathematics. To begin with, we will define what the area is and what figure is a hexagon, to later explain how the area is calculated in this case.
We will also pose a example so that you can understand it much better. At the end of the article you will also find exercises with their respective solutions, in order to clarify all doubts that may arise.
Index
- What is the area of a hexagon
- Tips for finding the area of a hexagon
- Example on finding the area of a hexagon
- Hexagon area calculation exercise
- Solutions
What is the area of a hexagon.
Before learning how to find the area of a hexagon, it is important that we understand the knowledge well.
In this way, the area is that calculation that allows us to know how much space it occupies an polygon concrete. In this case, since what we are learning is to calculate the
area of a hexagon, what we will do is quantify the space occupied by that hexagon.At this moment, we must remember and remember that the area is measured in units squared, so the result will be in m2, cm2, mm2...
A hexagon is a geometric figure that consists of six sides, this time we are going to establish that they are equal, so that we are facing a regular polygon. The sum of its angles will be 720º and it will consist of 6 equilateral triangles inside.
Tips for finding the area of a hexagon.
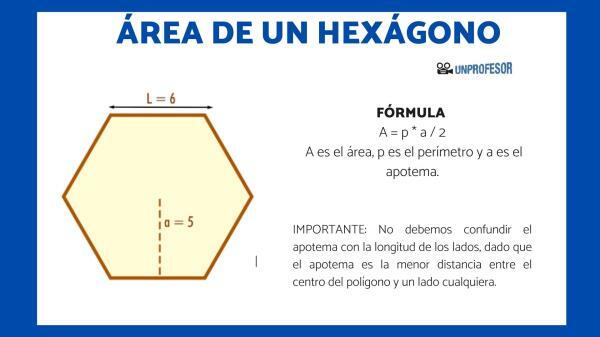
The main thing to calculate the area of a hexagon is to know the following formula:
- A = p * a / 2
- where A is the area, p is the perimeter, and a is the apothem.
Let's remember that the perimeter is the sum of all the sides, that is, the length of a side multiplied by six.
we must not confuse the apothem with the length of the sides, since the apothem is the smallest distance between the center of the polygon and any side.
In the hexagon, the apothem is identified as the line that goes from the center of the polygon to one of the sides perpendicularly, reaching the middle of that side, as in the image:
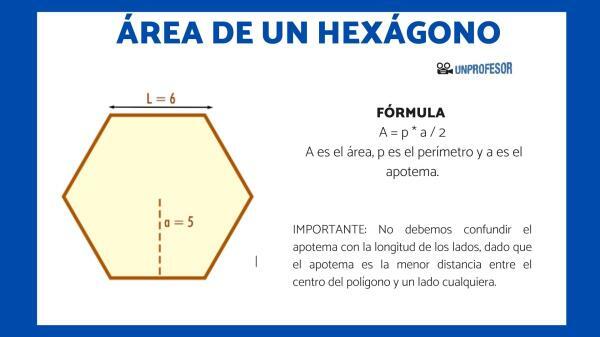
Example on finding the area of a hexagon.
We are going to calculate the area of the previous hexagon so that it is better understood. If we take into account that the sides of the hexagon are 3 meters and the apothem is 2.7 meters, we just have to apply the formula:
A = p * a / 2 = 18 * 2.7 / 2 = 24.3 square meters.
The important thing is to see where I got the p from, which is nothing more than multiplying the length of the side by 6, which is the total number of sides that a hexagon has.

Image: I am your teacher
Hexagon area calculation exercise.
To put into practice the knowledge acquired in this lesson, we suggest that you do some activities the answers to which you will find in the following section:
- 1. Find the area of a hexagon with a perimeter of 48 cm and an apothem of 7 cm.
- 2. Find the area of a rhomboid with a side of 8 mm and an apothem of 7 mm.
Solutions.
It is time to check that the activities have been carried out correctly:
1. Find the area of a hexagon with a perimeter of 48 cm and an apothem of 7 cm.
Since we are already given the perimeter and apothem, we can use the formula directly:
A = p * a / 2 = 48 * 7 / 2 = 168 square centimeters.
2. Find the area of a rhomboid with a side of 8 mm and an apothem of 7 mm.
A = p * a / 2 = 48 * 7 / 2 = 168 square millimeters. As you can see, the result is the same as in the previous exercise but in millimeters, given that if the side is 8, multiplying 8 by the 6 sides that the hexagon has, we are left with a perimeter of 48.
If you've come this far it's because you think this lesson is useful, so if you want to find more articles on math to continue learning, you just have to use the search engine at the top of the page Web. Don't forget to share this lesson with your classmates!
If you want to read more articles similar to How to find the area of a hexagon, we recommend that you enter our category of Geometry.



