Steps to remove the AREA of a CIRCLE with diameter

Discover how to find the area of ​​a circle with diameter! From a Teacher we bring you a new lesson in which we are going to explain how to get the area of ​​a circle having its diameter, which is important to have a basic understanding of mathematics and, specifically, of geometry. Therefore, we will start by defining what a circle is and what its diameter is. Next, we will analyze what area is and how to calculate it in this type of figure. Finally, we will solve an exercise that will serve as an example to check that the explanation has been understood.

A circle is a flat figure, that is, in two dimensions, it is formed by an edge called a circumference and an interior. Let's say that the circumference is the border, as if we take a rope and form a round figure, while the circle includes not only that rope, but also the inside.

It is considered to be a polygon with infinity sides, that is, it has so many sides that we can no longer see the vertices between them. In addition, it has infinite lines of symmetry. It has several elements, but the ones that interest us the most right now are the diameter and the radius. The first refers to the line that goes from any point on the border of the circle to its opposite point. The second, to the line that goes from the center to any point on the border.

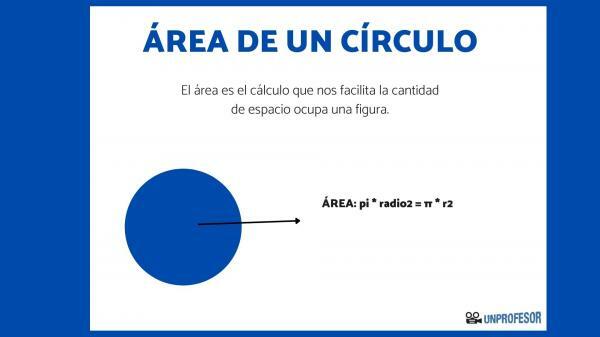
The areais the calculation that facilitates the amount of space a figure occupies. In our case, since we are talking about taking the area of ​​a circle, what we are doing is quantifying how much surface that circle occupies.

It is necessary to comment on one very important thing: area is always solved in squared units, so that, if we are given the data in meters, the area will be in meters squared. If we were talking about other polygons, I would also remind you that the units have to coincide, but since it is a circle, there will only be one unit that will refer to a measure of the polygon, which is why this point is indifferent to us now.

Once we know all this, we can now talk about how we are going to get the area of ​​a circle, since if you look for the formula online you will get that it is the following: pi * radio² = π * r2

But. What if instead of having the radius, what we have is the diameter? Well, we will simply use the following formula:

pi * (diameter / 2)², that is to say: π * (d / 2)²

This is so because the diameter is the distance between two opposite points on the edge of the circumference, while that the radius is half, because it is the distance between the center of the circumference and any point on the edge. Therefore, being half, we divide the diameter by two and we already have the radius.

It is necessary to emphasize that to simplify the resolution of these problems, we are going to consider that the number pi π is equivalent to 3.14, although, as you already know, it is a number with infinite decimal places.

Let's check if you have done the activities correctly:

1. Using the formula: pi * (diameter / 2)² = 3,14 * (2 / 2)² = 3,14 * 1² = 3,14 * 1 = 3,14. The solution is 3.14 cm².
2. Using the formula: pi * (d / 2)² = 3,14 * (5 / 2)² = 3,14 * 2,5² = 3,14 * 6,25 = 19,625. The answer is that it occupies a space of 19,625 m².
3. Again, using the formula: pi * (d / 2)² = 3,14 * (8 / 2)² = 3,14 * 4² = 3.14 * 16 = 50.24 cm².

If this article has been useful to you, remember that you can share it with your classmates and keep browsing a teacher's website to learn much more about mathematics and specifically upon Geometry.