Classification of ANGLES according to their sum

Welcome to the lesson of a Teacher in which we are going to explain the different types of angles that exist according to their sum, that is, we are going to carry out a classification of angles according to their sum. To do this, we will remember what an angle is and, next, we will proceed to develop the types that we find according to their sum. Finally, we will propose some activities with their respective solutions, so that you can check if you have understood what has been explained. Let us begin!

Index

1. What is an angle and elements
2. What is the classification of angles according to their sum
3. Examples of the classification of angles according to their sum
4. Exercise on complementary, supplementary and congruent angles
5. Solution

An angle is the opening resultant between two lines joined by a point called vertex or junction point. This opening can be measured in degrees or radians and the tool we recommend using for this is the protractor. Normally, this tool is a semicircle that can measure up to 180º, although sometimes it is a full circle and can measure up to 360º.

It is also necessary to comment that for each pair of lines that form an angle, in reality two angles are created (the interior and the exterior). The elements of an angle are:

• its two sides
• its two angles
• Its vertex or junction point.

The sides are actually two rays.

Angles are very practical mathematical elements, since we can find them in any place and moment of our lives: the corners of a goal form angles soccer, the slices of a pizza, the tilt of the tower of Pisa in Italy, the hands of an analog clock...

Angles can be of many different types, as we have already seen in other articles such as types of angles, but in this case we are going to talk about the classification based on the sum.

So we have this classification of angles according to their sum:

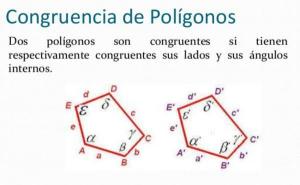
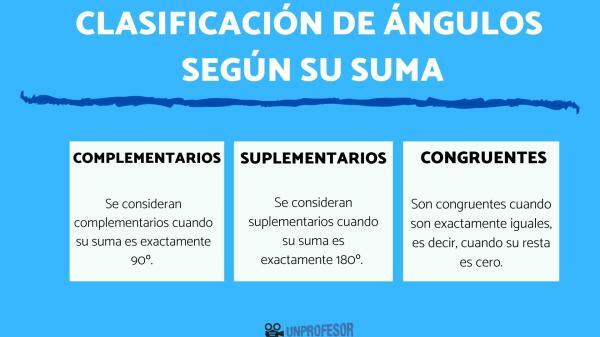
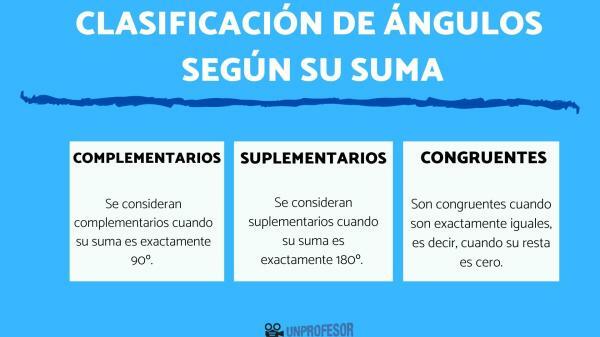
• complementary angles: a pair of angles are considered complementary when their sum is exactly 90º. To calculate a complementary angle, we will subtract 90 minus the angle that the statement tells us and it will give us its complement.
• supplementary angles: a pair of angles is considered supplementary when their sum is exactly 180º. They are calculated the same as the complementary ones, but taking the number 180 as a reference for the subtraction.
• congruent angles: a pair of angles are congruent when they are exactly equal, that is, when their difference is zero.

Thus, the classification is simple, we can find complementary, supplementary and congruent angles.

Let's look at some examples:

• Complementary angles: If we have an angle of 57º, its complement must be 33º, since 57 + 33 = 90. We can calculate it this way: 90 - 57 = 33.
• supplementary angles: if we have an angle of 70º, its supplementary will be 110º, since 70 + 110 = 180. We can calculate it like this: 180 - 70 = 110.
• congruent angles: it is simply the same number, that is, if we have an angle of 35º, its congruent will also be 35º.

We now propose that you solve the following exercises, so that you can check if it is clear to you what types of angles exist and what their measurements are. At the end of the article, you can find the answers.

1. Find the complementary angles of:

• 47º
• 12º
• 64º
• 59º
• 89º

2. Find the supplementary degrees of:

• 112º
• 23º
• 79º
• 95º
• 150º

3. Find the congruent degrees of:

• 28º
• 56º

Image: MundoPrimaria

1. Find the complementary angles of:

• 47º -> 43º, since 90 - 47 = 43.
• 12º -> 78º, since 90 - 12 = 78.
• 64º -> 26º, since 90 - 64 = 26.
• 59º -> 31º, since 90 - 59 = 31.
• 89º -> 1º, since 90 - 89 = 1.

2. Find the supplementary angles of:

• 112º -> 68º, since 180 - 112 = 68.
• 23º -> 157º, since 180 - 23 = 157.
• 79º -> 101º, since 180 - 79 = 101.
• 95º -> 85º, since 180 - 95 = 85.
• 150º -> 30º, since 180 - 150 = 30.

3. Find the congruent angles of:

• 28º -> 28º, since the angles are congruent if they have the same measure.
• 56º -> 56º, since the angles are congruent if they have the same measure.

If you have found this lesson useful, you can find many more by browsing the tabs or in the upper search engine. In addition, you can share it with your friends and classmates.

If you want to read more articles similar to Classification of angles according to their sum, we recommend that you enter our category of Geometry.

• Diaz Castillo, U. R. (2019). We measure and classify angles.
• Hernandez Gonzalez, O. AND. (2021). Angles.