Elements of a regular POLYGON

On this occasion, from a Teacher we are going to explain what are the elements of a regular polygon, aspect that we need to know, since it is basic knowledge for the study of mathematics and, specifically, of geometry. First, let's clarify concepts: what is a polygon and what are its elements. Next, we will see the characteristics of regular polygons. Finally, we will propose an exercise and its solution to check that the explanation has been understood.
A polygon It is that figure that we draw in plane geometry and that has a specific number of sides, so that it encompasses a finite region of the plane. The sides are the segments of the figure and the place where they join each other are the vertices or, more commonly said, the corners. Two angles are created at each vertex: interior and exterior.
In this way, the elements of a regular polygon are:
- The sides that form the segments of the figure, also called edges or sides, which must always be straight.
- The vertices or corners, which are the joining points of two sides. On occasion, they can also be the point of intersection, if the sides intersect.
- The angles, which can be interior or exterior. The interiors are constituted by the amplitude left by the vertex that joins two consecutive sides. The exteriors are constituted by one of the sides and the extension of the consecutive side by the exterior of the polygon.
- The diagonals, which are the lines that connect two non-consecutive vertices of the polygon.
- The center, which is the internal point of the polygon that is the same distance from all vertices and sides.
- The central angle, which is formed by two segments that go from the center to the ends of a side.
- The apothem, which is the line that joins the center of the polygon with the center of one side.
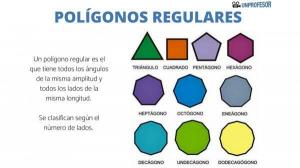
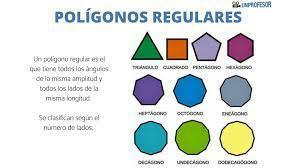
Here are some good ones examples of regular polygons:
- Equilateral triangle: has 3 sides.
- Square: has 4 sides.
- regular pentagon: it has 5 sides.
- regular hexagon: has 6 sides.
- regular heptagon: has 7 sides.
- regular octagon: has 8 sides.
- regular nonagon: has 9 sides.
- regular decagon: has 10 sides.
- regular hendecagon: has 11 sides.
- regular dodecagon: has 12 sides.
- regular tridecagon: has 13 sides.
- regular tetradecagon: has 14 sides.
- ...
Only the first two polygons mentioned (equilateral triangle and square) have their own name, since that the others have simply taken the name of the figure with those sides with the last name "regular" behind.
To finish the lesson and you can see if you have learned the explained concepts about the elements of a regular polygon, here we leave you the proposed exercise to check it.
1. Distinguish true sentences from false sentences:
- Regular polygons always have a center.
- The sides of regular polygons can be straight or curved.
- Regular polygons, unlike irregular polygons, only have internal angles.
- A circle can be inscribed in all regular polygons.
Let's check if you have carried out the proposed activities correctly:
1. Distinguish true sentences from false sentences:
- Regular polygons always have a center: true.
- The sides of regular polygons can be straight or curved: false, they can only be straight.
- Regular polygons, unlike irregular ones, only have internal angles: false, they have internal and external angles.
- A circle can be inscribed in all regular polygons: true.
If this lesson has helped you improve your learning of polygons, keep browsing the web to read other articles. In addition, you can use the search engine at the top to find everything you need.