How to get the AREA of a right TRIANGLE

Again, a Professor brings another math lesson, this time on how to find the area of a right triangle, thus reviewing elementary concepts when learning geometry. To begin, we will see the concept of a triangle and, specifically, a right triangle. Next, we will clarify what an area is and how to calculate it in this particular polygon. Lastly, we provide training monitoring and its solutions to verify if the explained has been understood.
Index
- What is a right triangle?
- Calculating the area of a right triangle
- Exercise to find the area of a right triangle
- Exercise solutions
What is a right triangle?
Before discovering how to find the area of a right triangle, it is important to know what this type of geometric figure is.
A triangleis he polygon composed of three edges (sides), three vertices and three angles, but they do not have to be equal between them, it is that is, they can be triangles of different types, since the sides can have different lengths or the angles different opening.
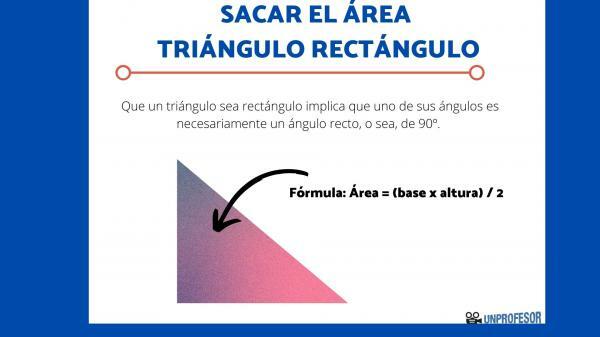
Therefore, the triangles can be equilateral, obtuse, rectangles... It is on the latter that we are going to focus. That a triangle be right implies that one of its angles is necessarily a right angle, that is, 90º. If you need to review the different angles that exist, we recommend the article Types of angles.
Having such a clear structure, its sides also have a name: the side opposite the right angle is called hypotenuse, while the other two are the legs. In this way, a right triangle is easily identifiable, since if we put another rotated triangle that fits the hypotenuse, we will obtain a square.
Calculation of the area of a right triangle.
To find the area of a right triangle we must know that a area is the formula that calculates how much space does it occupy a figure, so that the area of a right triangle quantifies how much surface area that polygon occupies.
It should be noted that the area has to be calculated in squared units, so if the data is in centimeters, the area will be in centimeters squared. For this, it is essential that the units coincide, so if one side of the figure is in meters, the other must also be and, if it is not, we must pass it to unify the units. This is obligatory.
When these points are clear, we can calculate the area of a right triangle through the following formula:
- Area = (b x h) / 2
- Where b = base; h = height.
In this case, the base and the height will be legs, never the hypotenuse. That is, we do not need to know how long the hypotenuse is to be able to calculate the area, just having the length of the legs is enough. However, if they give you the hypotenuse and a single leg, you can calculate how long the other leg is based on the Pythagoras theorem.
In short, to calculate the area of a right triangle, we will multiply what the two legs measure and the result will be divided by two.
Exercise to find the area of a right triangle.
Let's do now training to see if you understand today's lesson on how to find the area of a right triangle. In the next section you will see the solutions so that, thus, you can put your knowledge to the test:
- Find the area of a right triangle 5 centimeters in base and 7 centimeters in height.
- Find the area of a 10-meter right triangle on both legs.
- Calculate the area of a triangle that has an angle of 90º, knowing that the sides adjacent to that angle are 6 centimeters and 9 centimeters each.
Solutions of the exercises.
We are going to correct the activities you just did:
- Following the formula, we multiply the base times the height and divide by two: (5 x 7) / 2 = 35/2 = 17.5 centimeters squared = 17.5 cm2.
- Again, if we follow the formula, since the base and the height are just the legs, we multiply both legs with each other and divide by two: (10 x 10) / 2 = 100/2 = 50 meters at square = 50 m2.
- As the statement tells us that the triangle has an angle of 90º, we already know that we are dealing with a right triangle, so that the sides that form that angle are the legs. Therefore, we can reuse the formula mentioned in the previous exercises: (6 x 9) / 2 = 54/2 = 27 cm2.
If you have found it interesting and want to read more articles similar to this, we recommend that you browse the web search engine, specifically in the category of Geometry and in the section of Perimeters and areas.
If you want to read more articles similar to How to Find the Area of a Right Triangle, we recommend that you enter our category of Geometry.