What are CONGRUENT polygons?

In this lesson that we bring you from a Teacher, you will be able to understand what are congruent polygons with examples. To begin with, we will define concepts and see what movements we can make to make some polygons congruent. Then, we will propose an exercise and its respective solution. Let's go there!

Index

1. What are congruent polygons?
2. How to know if the polygons are congruent?
3. Example of congruent polygons
4. Congruent Polygons Exercise
5. Solution

That two polygons are congruent means that they have congruence, but what does that mean? Well, basically it is the logical relationship that is established between different things, in this case, the logical relationship established between different polygons.

Thus, in mathematics, two geometric figures will be congruent if they both have the same dimensions and identical shape, regardless of the position or orientation of the figure in question.

In other words, there must be an isometry that relates the figures.

On the other hand, in this article we are going to talk about congruent polygons, so we will not refer to any shape, but only to polygons. That is, any shape can have its congruent, but we will focus on congruent polygons.

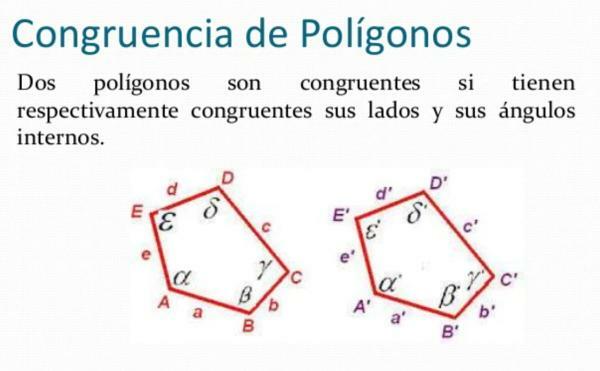
Image: Slideshare

For the polygons to be congruent we can perform different transformations. These can be from translation, rotation and reflection. In addition, these transformations can be combined by doing several at the same time.

• Translation: consists of moving a polygon from one location to another, but without changing its size, shape or orientation.
• Rotation: consists of rotating each point of the polygon through the specified angle and direction around a fixed point, called the center of rotation.
• Reflection: consists of reflecting the image as if it were a mirror, using a line of reflection in the established direction.

here we leave you examples of congruent polygons so that you better understand what we are indicating.

In this image, we can see each movement in a different figure. In the first box, the polygon has been moved from one place to another, without changing its orientation or rotating it, so they are congruent. In the second, the polygon is the same, but we've rotated it, so they're also congruent. In the third, as if it were a mirror, we have reflected the polygon, so they are also congruent.

As you have seen, here we have made movements with different polygons, but we can take the same polygon and first translate it and then rotate it, reflect it... There are many options.

So that you can practice what we have discussed in this article, we leave you these activities:

1. Decide if the following sentences are true or false:

• Reflection consists of reflecting horizontally, as if we put a mirror and the reflected figure was left or right.
• Translation involves moving the figure from one place to another on the plane, without changing the shape of the figure.
• Two polygons are only congruent if we translate, rotate, or reflect them, but not if we do more than one of these things at the same time.

2. Draw a square of two centimeters on a side in the upper left quadrant of the plan, attached to the axes, and make simultaneously the three movements explained in the lesson: first move the polygon one centimeter to the left and above. Next, rotate the square 90º and reflect it with a reflection line located on the horizontal axis.

Let's see the answers:

1.

• Reflection consists of reflecting horizontally, as if we were placing a mirror and the reflected figure remained on the left or right: FALSE, because the reflection can be both horizontal and vertical, as in any address.
• The translation implies moving the figure from one place to another in the plane, without changing the shape of the figure: TRUE.
• Two polygons are only congruent if we translate, rotate, or reflect them, but not if we do more than one of them. these things at the same time: FALSE, we can make several movements at the same time and they would still be polygons congruent.

2. The square must be in the lower left quadrant, but with exactly the same shape, since when we rotate a square 90º we still have exactly the same shape with the naked eye.

If you found this post interesting, don't forget to comment and pass it on to your classmates, in addition to browsing the multiple tabs on the web.

If you want to read more articles similar to Congruent polygons - with examples, we recommend that you enter our category of Geometry.