How to get the DIAMETER of a circle

To get the diameter of a circle you can take into account two values: radius or circumference. In unProfesor we tell you the two techniques with examples.

In a new lesson from a Teacher we will work on how to get the diameter of a circle. Starting with the concept of a circle, followed by what is the diameter of a circle and ending with the calculation of the diameter. To finish we will do some examples and exercises on the topic.

Index

1. What is the diameter of a circle
2. How the diameter of a circle is calculated - with examples
3. What is a circle?
4. Exercises

One of the most important parts of the circle is the diameter. The diameter of a circle is the measure of the ray drawn from any of the points from the circumference to another point and passing through the center of the circle.

Since the measure of the diameter is always the same, then we can always divide into two equal parts to any circle.

On the other hand, we can ensure that

The ratio of the circumference of a circle to its diameter is the number π.

So if C is the circumference of a circle and d its diameter, we have:

C/d = π

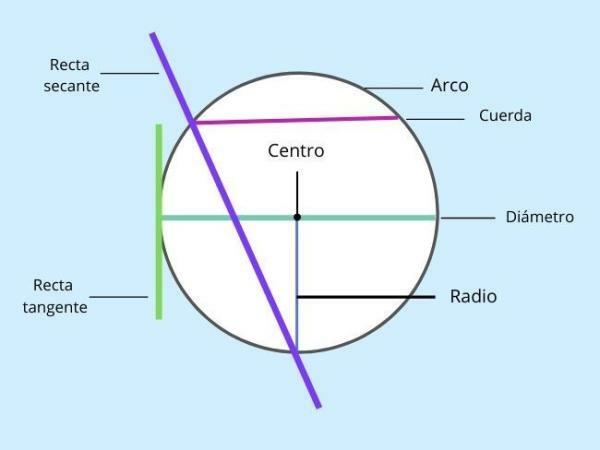
Image: Differentiator

To calculate the diameter of a circle, we must have as data some of its other measures or dimensions. That is to say, we must know the radius or circumference.

1-Knowing the radius

As we saw previously, the diameter is twice the radius, so knowing the value of the measure of the radius, we can obtain the diameter by multiplying it by two.

So if r is the radius and d is the diameter:

d = 2 x r

2- Knowing the circumference

As we saw in the concept of diameter, the ratio between the circumference and the diameter is equal to π, therefore we clear the diameter from the equation and obtain the result.

• C/d = π
• C / π = d

Examples of how to get the diameter of a circle

Let be a circle of radius 5 cm. Calculate the diameter.

Knowing that the diameter is twice the radius, we use the formula and obtain the result.

• d = 2 x r
• d = 2 x 5
• d = 10cm

The diameter of the circle is 10 cm.

Let be a circle with a circumference of 25 cm. Calculate its diameter.

If we know the measure of the circumference of the circle, we use the option two formula and calculate

• C/d = π
• C / π = d
• 25 / π = d
• d = 7.95cm

So the measurement of the diameter is 7.95 cm

In this other lesson we tell you how to get the area of ​​a circle with diameter.

A circle, within geometry, is a figure that is found bounded by the circumference, this being the line that forms the limit or outline of our circle. The circle then is the area that forms or contains a circumference.

There is then a difference between circle and circumference due to its definition. While the circumference is the curved line that forms or delimits a figure, the circle is the area or surface that is contained in that line.

In addition, we can say that the circle is a two-dimensional figure that is represented by a curved line called the circumference, being this closed, and in which any of its points will have the same length of distance with the center of the circle.

parts of a circle

The parts that form a circle are the following:

• Circumference: curved line that delimits the circle, that is, its border, its contour.
• Center: is the point that is in the middle of the circle, that is to say that it has the same distance in all its points.
• Radio: is the ray that joins the center of the circle with any point on the circumference.
• Diameter: is the ray that joins two opposite points of the circumference and that passes through the center of the circle.
• Rope: is the ray that joins any two points on the circumference and does NOT pass through the center. The measure of the chord is always less than the measure of the diameter.
• Arc: It is a part of the circumference that is measured between any two points of the same.

Here we leave you exercises so you know how to get the diameter of a circle. You will also find solutions so you can practice at home.

Exercise 1

say if it is true and false

1. The diameter of a circle is the measure of 3 radii.
2. The circle is the surface bounded by the circumference.
3. The radius of a circle is equal to the measure of the chord.
4. The diameter is the line that passes through the center and joins two points on the circumference.
5. The ratio between the circumference and the diameter is equal to π.
6. You can calculate the diameter of a circle by knowing the measure of the arc.
7. The chord and the diameter are of the same measure.

Solution

1. Fake. The diameter of a circle is twice the radius.
2. TRUE.
3. Fake. The radius is the distance from any point on the circumference to the center of the circle, while the chord is the union of any two points of the circumference that do NOT pass through the center.
4. TRUE.
5. TRUE.
6. Fake. You can know the diameter of a circle by knowing the value of the radius or the circumference.
7. Fake. The measure of the chord will always be less than the diameter.

Exercise 2

Calculate.

1. Calculate the diameter of the circle, the radius being 6 cm.
2. Calculate the diameter of the circle, the circumference being 65 cm.
3. Calculate the diameter of the circle, the circumference being 32 cm.
4. Calculate the diameter of the circle, the radius being 14 cm.

Solution

1-Knowing that the diameter is twice the radius, we use the formula and obtain the result.

d = 2 x r

d = 2 x 6

d = 12cm

The diameter of the circle is 12 cm.

2-If we know the measure of the circumference of the circle, we use the formula of option two and calculate

C/d = π

C / π = d

65 / π = d

d = 20.69cm

So the measurement of the diameter is 20.69 cm.

3-If we know the measure of the circumference of the circle, we use the formula of option two and calculate

C/d = π

C / π = d

32 / π = d

d = 10.18cm

So the measurement of the diameter is 10.18 cm.

4-Knowing that the diameter is twice the radius, we use the formula and obtain the result.

d = 2 x r

d=2 x 14

d = 28cm

The diameter of the circle is 28 cm.

If you liked this lesson, share it with your classmates. And remember that you can continue browsing the page. On the website of a Teacher there is very interesting content that can be useful to you.

If you want to read more articles similar to How to get the diameter of a circle, we recommend that you enter our category of Geometry.