How to find the height of a scalene triangle
In this new lesson from a Teacher we are going to see how to get the height of a scalene triangle. We will start with the concept of triangle, we will see its types and what are the different scalene triangles that exist. Then we are going to calculate how to get the height of the scalene triangle and an example.
The height of the triangles are those perpendicular segments to one of its sides that starts from the vertex opposite the side in question. In other words, it is the distance between one side and its opposite vertex.
That being said, we know that each triangle has three heights, since it has three sides and three vertices.
The easiest method to get the height of a scalene triangle is using the formula for the area of a triangle and clearing the height of the equation. But the drawback of this formula is that we must know the value of the area to solve it.
Let's see...
A = (b x h)/2
A is the area of the triangle, b is the base, and h is the height.
We clear h from the equation and obtain:
h = (A x 2) / b
To solve the height of any type of triangles we will use Heron's formula, with which the semi-perimeter of a triangle is calculated with the measure of its sides.
We will call a, b and c the sides of the triangle and s the semiperimeter of this and it is calculated:
s = (a + b + c)/2
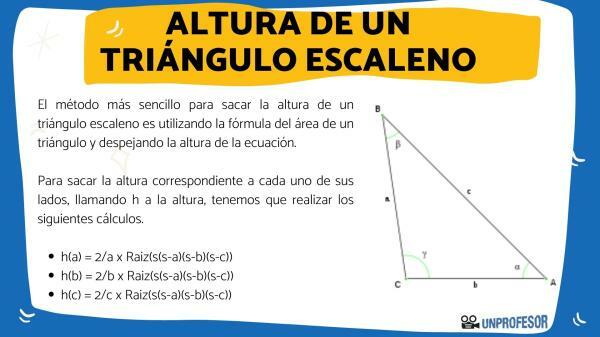
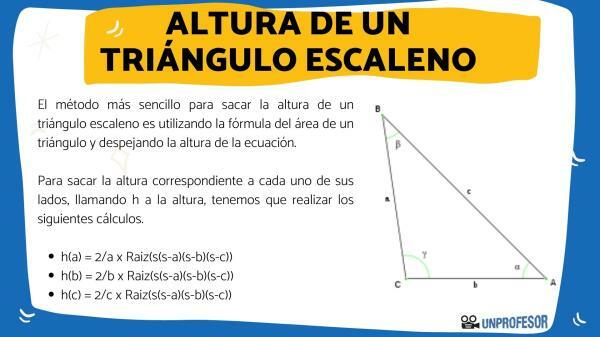
So, to get the height corresponding to each of its sides, calling the height h, we have to perform the following calculations.
- h (a) = 2/a x Root (s(s-a)(s-b)(s-c))
- h (b) = 2/b x Root (s(s-a)(s-b)(s-c))
- h (c) = 2/c x Root (s(s-a)(s-b)(s-c))
We have a scalene acute triangle with sides measuring 3 cm, 4 cm and 5 cm. We want to calculate the height corresponding to each of its sides.
We first calculate the semiperimeter
s= (3 + 4 +5)/2 = 12/2 = 6
Then we set up the equations of the heights each
- h (3) = 2/3 x Root (6(6-3)(6-4)(6-5)) = 4
- h (4) = 2/4 x Root (6(6-3)(6-4)(6-5)) = 3
- h (5) = 2/5 x Root (6(6-3)(6-4)(6-5)) = 2.4
The heights then are 4cm, 3cm and 2.4cm
Do you still have doubts? At unProfesor we help you!
Now that you know how to get the height of a scalene triangle, we are going to review some theoretical concepts that will help us better understand this lesson.
A triangle is a polygon that is made up of three sides, three vertices and three angles.
Triangles, in mathematics, are very important figures, since they are the basis of other types of polygons. The sum of the interior angles of triangles ALWAYS adds up to 180° sexagesimals.
The elements of a triangleare:
- sides: are the lines or half lines that delimit the figure and join the vertices of it.
- vertices: are the unions that are formed between one side and the other, that is, the points that connect the sides of the triangle.
- interior angles: are the angles that are formed in the interior with the union of two sides, that is, the amplitude in the interior of two sides.
- exterior angles: are the angles that are formed on the outside of the triangle with the union of two of its sides, that is, the amplitude on the outside of two sides.

Triangles are shapes that can qualify according to their angles or sides.
According to their sides the triangles can be:
- Equilateral: its three sides measure exactly the same.
- Isosceles: two of its sides are exactly the same length, while the other is not.
- Scalene: its three sides have different measurements.
Depending on their angles, triangles can be:
- rectangles: one of its interior angles measures exactly 90° sexagesimals. The sides that make up that angle are called legs, while the opposite of it is called the hypotenuse.
- oblique: none of its interior angles is right, that is, none measures 90° sexagesimals. They may be:
- obtuse angles: one of its interior angles measures more than 90 sexagesimal degrees, that is, it is obtuse, while the other two angles are acute and measure less than 90 sexagesimal degrees.
- acute: all its interior angles are acute, they measure less than 90 sexagesimal degrees.
These two classifications can be combined and form different triangles.


