How to get the AREA and VOLUME of the CONE

This lesson that we bring you from a Teacher is about how to find the area and volume of the cone, an essential lesson for a more advanced study of geometry and, therefore, of mathematics. So let's start by clarifying the concepts of cone, area and volume, to later see how to remove these last two. In the end, we will propose a exercise and its respective solution.

Index

1. What is a cone, its area and volume
2. How to find the area of ​​a cone - with example
3. How to find the volume of a cone and examples
4. Exercise to find the area and volume of a cone
5. Solution

a cone is that geometric figure in three dimensions which is created by wrapping a triangle around one of its sides. In this way, the cones have a circular base. This geometric body is considered a body of revolution.

has different elements:

• Circle base.
• Vertex: is the upper peak.
• Generatrix: is what measures the side of the cone, from one end of the circular base to the vertex.
instagram story viewer
• Height: goes from the center point of the base circle to the vertex. It should not be confused with the generatrix.

The area is the calculation that allows know the space that a polygon occupies determined in two dimensions. As in today's lesson we are studying the area of ​​a cone, we will be quantifying the space that cone occupies if we unfold it, so that it is in two dimensions. Let's say the area is the "edge" of the figure. It is always expressed in units squared (m², km²...).

Volume is the space it occupies in three dimensions. that polygon, so we can understand that it is the "filled" figure. It is always expressed in units cubed (m³, km³...).

Image source: Slideshare

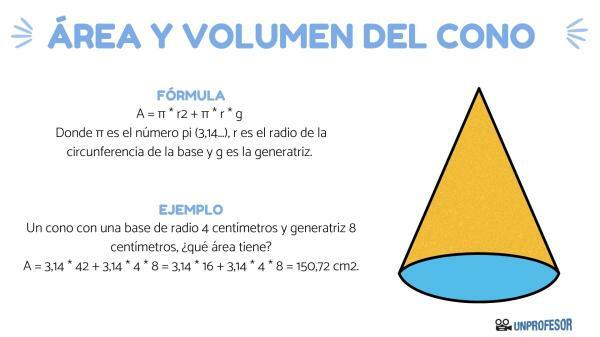
Let's see how to calculate the area of ​​the cone. As it is a threedimensional Figure, if we unfold it in two dimensions, we are left with a circle and a kind of triangle, so we will have to calculate the area of ​​each of these parts. The formula is:

A = π * r² + π * r * g

Where π is the number pi (3.14...), r is the radius of the circumference of the base and g is the generatrix.

Example

Let's look at an example:

A cone with a base of radius 4 centimeters and a generatrix of 8 centimeters, what area does it have?

A = 3.14 * 4² + 3,14 * 4 * 8 = 3,14 * 16 + 3,14 * 4 * 8 = 150.72cm².

Let us now see how the volume of the cone is calculated. The formula is:

V = (π * r² * h) / 3

Where π is the number pi (3.14...), r is the radius of the circumference of the base and h is the height.

Example

Let's look at an example:

What is the volume of a cone with a base of radius 4 centimeters and a height of 12 centimeters?

V = (3.14 * 4² * 12) / 3 = (3,14 * 16 * 12) / 3 = 200.96cm³.

Remember that the diameter is twice the radius, so if we are given the diameter, what we have to do is divide it by two to find the radius.

Let's see if the explanation is clear with the following exercises. Below you will find the solution.

1. Calculate the area of ​​a cone with the following measurements (in centimeters):

• Radius 7 and generatrix 20.
• Radius 1 and generatrix 8.

2. Calculate the volume of a cone with the following measurements (in meters):

• Radius 3 and height 15.
• Radius 7 and height 18.

Here you will find the response to previous activities, so you can check if you have done them correctly:

1. Area

• Radius 7 and generatrix 20: A = 3.14 * 7² + 3.14 * 7 * 20 = 593.46cm².
• Radius 1 and generatrix 8: A = 3.14 * 1² + 3.14 * 1 * 8 = 28.26cm².

2. Volume:

• Radius 3 and height 15: V = (3.14 * 3² * 15) / 3 = 141.3m³.
• Radius 7 and height 18: V = (3.14 * 7² * 18) / 3 = 923.16m³.

If you have come this far it is because you consider this lesson to be useful, so if you want to find more articles on mathematics that are useful to you, you just have to use the search engine at the top of the page Web.

If you want to read more articles similar to How to get the area and volume of the cone, we recommend that you enter our category of Geometry.