What are convex and concave polygons

In the lesson that we bring you today from a Teacher you will be able to understand the Differentiate between convex and concave polygons using examples. On other occasions we have developed lessons on the classification of polygons into regular or irregular, but today we will follow another criterion, as you will be able to see below. In addition, at the end of the post you will be able to do an exercise and check if you have done it correctly with its solutions.
Index
- What are polygons in mathematics
- What are concave polygons
- What are convex polygons
- Examples of Concave and Convex Polygons
- Exercise
- Solution
What are polygons in mathematics.
Let us remember that polygons are flat figures with a certain number of sides that encompass a region of a plane of finite form (they are not infinite). Those sides that form the segments of the figure are known as edges and the point where two edges meet is called the vertex or corner.
At each of those vertices
two angles are generated, the interior and the exterior, which is simply the amplitude generated at the vertex.Well, the latter is key to understanding the classification that we are going to make today: the interior angles. Depending on their amplitude, the polygons can be convex or concave.
What are concave polygons.
For a polygon to be considered concave, at least one of its interior angles must be concave, that is to say, greater than 180º.
This converts all concave polygons to irregular polygons, since they can never have all their angles equal, although they can be equilateral: their sides can have the same length.
An important point that we must emphasize is that a figure cannot have more concave than convex angles, at most it can have half of each.
Star polygons: special concave polygons
Also noteworthy is a particular class of concave polygons: star polygons. This type of polygon is actually called enneagrams, but because of their star shape they are commonly known as stellate.
Half of their interior angles are convex and half concave, so they always have an even number of sides. They are always symmetrical and equilateral, since their sides have the same length as each other. In fact, enneagrams are formed with the diagonals of regular polygons. For example, a pentagram is a five-pointed star formed from the diagonals of a regular pentagon.
What are convex polygons.
On the other hand, if it is a convex polygon, all interior angles must be convex, that is to say, less than 180º. This implies that all regular polygons are convex, but not all convex polygons are regular. In other words: convex polygons can be regular or irregular, but regular polygons will always be convex, never concave.
Also, in convex polygons you can draw a line from any part of the figure to any part of the figure and you will always be inside it, however in concaves there may be lines that come out of the figure to get from part to other.
Think in a circle: you can always go from one part to another, without leaving the circle; but if it were a donut, if you went from one side to the other you would come out through the hole. In this case, the circle refers to the convex polygons and the donut refers to the concave ones.
Examples of concave and convex polygons.
To finish understanding this lesson on concave and convex polygons, we will leave you here some examples that will help you understand it better.
- Some examples of concave polygons they are a thick arrow or stairs on the inside.
- Some examples of convex polygons They can be a yield sign, a blackboard, or the holes in a hive (hexagonal).

Exercise.
To check if you have understood the difference between convex polygons and concave polygons, we are going to carry out the following exercise:
- Specify which shapes are convex polygons and which shapes are concave polygons.
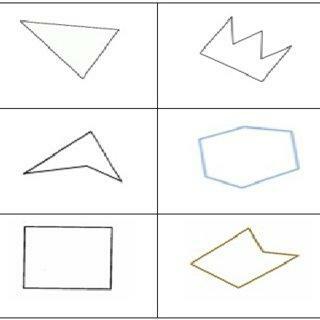
Solution.
Now let's check if you have done the activity set out in the previous section correctly:
- The convex polygons are the triangle, the hexagon and the square (figures 1, 4 and 5), while the concave polygons are the crown, the arrowhead and the irregular pentagon (figures 2, 3 and 6).
If you have understood well the classification of polygons into concave and convex, you will surely want to continue browsing the Geometry tab. If, on the other hand, you want to find lessons on other subjects, you can use the search engine that you will find at the top of the web.
If you want to read more articles similar to Convex and concave polygons - examples, we recommend that you enter our category of Geometry.