SCALEN triangle: characteristics and formula

In this new article by a Professor we bring you a basic lesson for the study of geometry: the characteristics of a scalene triangle and the formula to get your area. First, we are going to recall the concepts of triangle and scalene. Next, we will explain what the area is and how to calculate it in this polygon that we are studying. Lastly, we are going to raise a exercise and we will give you the solution, to verify that you have acquired the new knowledge.
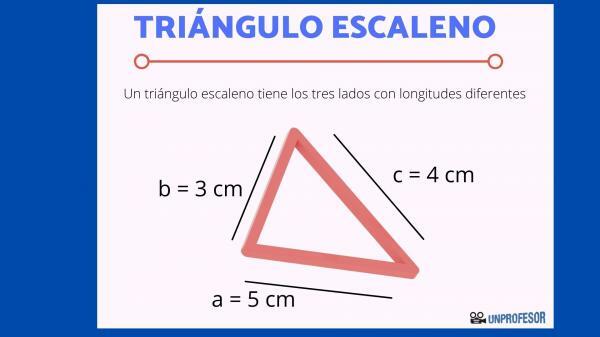
A triangle is the polygon with three edges or sides, three vertices and three angles, so there may be triangles of different types, being able to have the sides of different lengths or the angles of different amplitude.
Just as an equilateral triangle was one that had all its sides and angles equal, as we already explained in the the corresponding lesson, a scalene triangle is exactly the opposite: it is the one that has absolutely all sides and angles of varying length and width.
However, the condition is maintained that the sum of the angles of a triangle gives 180º, but in this case each of the three angles will be different.
Prior to calculate areaLet's see what that word means. The area is the calculation we do to find out how much space does a figure occupy. In this way, the area of a scalene triangle will tell us how much surface that triangle occupies. Remember that the area is always solved in units squared, so if we are given the data in centimeters in the statement, we will calculate the area and solve it in centimeters squared. The same happens if they provide us with the statement in meters, since we will solve the area in meters squared.
It is very important to mention that to calculate the area of any polygon, it is mandatory have the units in the same measure. This means that if one side of the figure is in meters, the other sides must also be in meters. If they weren't and they were, for example, in kilometers, we should unify those measurements to be able to calculate the area passing meters to kilometers or kilometers to meters.
When we have all this ready, we can begin to calculate the area of our scalene triangle with the following formula:
- Area = (b x h) / 2
- Where b = base; h = height.
What you need to do is simply multiply the base of the triangle by its height, which is the line that crosses from the vertex to the base, and then divide by 2. The most complicated thing is to find the height, since they will not always provide it to us in the statement directly.
Calculate the height of a scalene triangle
To find the height of a scalene triangle, we could apply the Pythagoras theorem. What we will do is divide the triangle in two by marking a line that goes from the vertex to the base, that is, marking the height. So, we will be left with two right triangles. Using any of them, we apply the formula of the Theorem, the height we want to know being a leg.
If this way of calculating it seems complicated, don't worry, because we have an alternative. The alternative formula is the next:
- Area = (sp x (sp - a) x (sp - b) x (sp - c))1/2
- Where sp = semiperimeter = (a + b + c) / 2; a = side 1; b = side 2; c = side 3.
What should be done here is to calculate the semiperimeter by adding the three sides and dividing the result by 2. Then we subtract side 1 from the semiperimeter and keep that number. We do the same with sides 2 and 3. Finally, we will multiply those numbers that we had saved with each other and by the semiperimeter and we will raise the result to a half or we will take the square root.

To finish this lesson, we are going to offer some scalene triangle exercises to help you put yourself to the test. They are as follows:
- Find the area of a scalene triangle with base 6 m and height 3 m.
- Find the area of a scalene triangle with sides 7 cm, 5 cm, and 3 cm.
Finally, we leave you the solutions to the previous exercise that will allow you to check if, really, you have understood this lesson well.
Exercise 1 solution:
This exercise is simple, since they give us the base and the height directly, so we just have to apply the formula:
(6 x 3) / 2 = 18/2 = 9 m2.
Exercise 2 solution:
Since we know the three sides, we apply the alternative formula. First, we calculate the semiperimeter:
sp = (7 + 5 + 3) / 2 = 15/2 = 7.5
With side 1: 7.5 - 7 = 0.5; with side 2: 7.5 - 5 = 2.5; with side 3: 7.5 - 3 = 4.5.
Area = (0.5 x 2.5 x 4.5 x 7.5)1/2 = 42,18751/2 = 6.5 cm2.