Remove the AREA from an IRREGULAR RECTANGLE

On this occasion, from a teacher we are going to explain to you how to get the area of ​​an irregular rectangle, a very important lesson for the study of mathematics and, specifically, geometry. First of all, we will clarify concepts: what is a rectangle and what makes it irregular. Once this is clear, we will see what area is and how to calculate it in this type of figure. Finally, we will solve a exercise to serve as an example to verify that the explanation has been understood.

Index

1. What is an irregular rectangle?
2. Steps to Calculate and Find the Area of ​​an Irregular Rectangle
3. Exercise to calculate the area of ​​an irregular rectangle

Before showing you how to find the area of ​​an irregular rectangle, it is important that we define the mathematical term so that you can better understand this lesson.

If we had to define what is a rectangle in a simple way, we would say that it is that flat figure that has four sides

From the definition itself it follows that not all sides are the same, so a rectangle is never going to be considered a regular polygon. In other words, since two sides are different from the other two, a rectangle will always be irregular. The only four-sided figure that is regular is the square. In this sense, calling this figure an irregular rectangle is redundant, so from now on, we are going to call it simply a rectangle.

Differences between rectangles and quadrilaterals

Do not confuse the rectangles with the others quadrilaterals, since all the figures with four sides and four vertices are quadrilaterals, but not all are rectangles (they can be rhombuses, trapezoids, trapezoids, rhomboids ...). It should be clear that, for a figure to be considered a rectangle, it must meet the aforementioned requirements: the sides must be parallel and equal two by two and the angles must be right.

In addition, on numerous occasions, it's easy to make mistakes and confuse the irregular rectangles with the irregular quadrilaterals, which are those figures with four sides, all of them different, joined by angles also of different amplitude.

The area is that calculation that allows to discover how much space does a figure occupy. In our case, since we want to get the area of ​​an irregular rectangle, we will be quantifying how much surface that rectangle occupies. It is important to remember that the area always occurs in squared unitsTherefore, if we are given the data in centimeters, the area will be in centimeters squared.

It must also be taken into account that, in order to calculate the area of ​​the polygon, whether it is regular or irregular, the units must match. In this way, if one side is given in meters and the other in centimeters, we will have to unify it to be able to calculate the area.

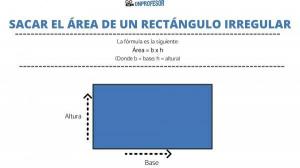
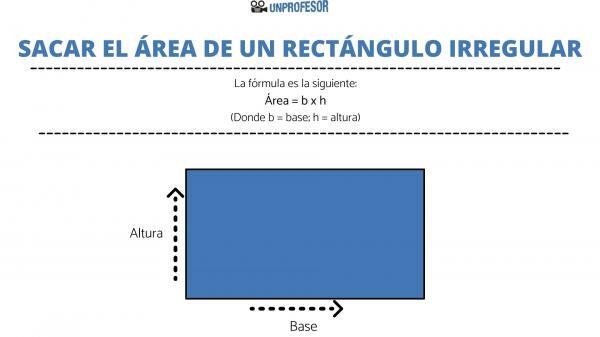
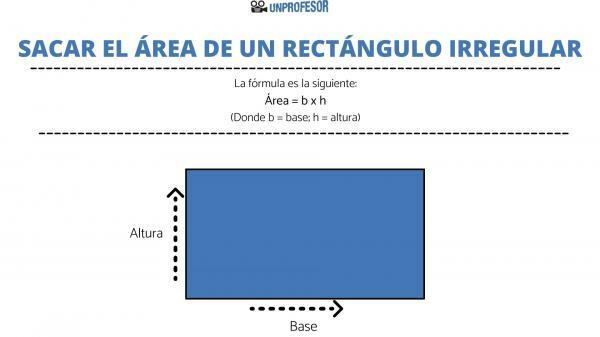
At this point, we can calculate the area of ​​a rectangle. The formula is as follows:

• Area = b x h
• Where b = base; h = height.

Ultimately, what you have to do is simply multiply one of the sides by the other that is not its parallel, that is, multiply the base times the height, taking into account that the units of measurement are the same.

Let's see now a resolved exercise that you can take as an example to get the area of ​​a rectangle.

• Height: h = 6 centimeters
• Base: b = 3 centimeters

So, we apply the formula, which tells us that we have to multiply the base times the height:

Area = 6 centimeters x 3 centimeters = 18 centimeters squared

In this example, the area is 18 cm².

More tips for calculating the area of ​​an irregular rectangle

We are going to highlight two issues. The first is that the result will always be in squared units, as we have already let you know before. The second is that, if any of the measurements were not in centimeters, we would have to unify units. Let's see an example:

• Height: h = 6 centimeters
• Base: b = 200 millimeters

The first thing we will do is either change the centimeters to millimeters, or change the millimeters to centimeters. In this case, I will follow the second option: since 1 centimeter is 100 millimeters, 200 millimeters will be 2 centimeters.

We transform the data:

• Height: h = 6 centimeters
• Base: b = 2 centimeter

Area = 6 centimeters x 2 centimeters = 12 centimeters squared

In this case, we obtain an area of ​​12 cm².

If you have come this far, you already understand how to calculate the area of ​​a rectangle. This calculation is very Useful in everyday life, as it is used for situations as common as calculating the surface of a room or calculating how much lawn area we can put in a patio.

If you are interested in learning more about geometry, you can continue browsing our website, where you will find lessons and videos to understand everything you want to know. We encourage you to do so!

If you want to read more articles similar to How to get the area of ​​an irregular rectangle, we recommend that you enter our category of Geometry.