What is the DENOMINATOR and examples

In this new lesson from a math teacher you will learn what is the denominator, a very important aspect to understand how operate with fractions. It is an agenda that is used continuously in the subject of mathematics. We will start by defining what the denominator is and we will see examples so that everything is understood correctly. After that, we will analyze what the common denominator means. Finally, we will see exercises with their respective solutions.
The denominator is the bottom of a fraction or, what is the same, the number of parts into which the unit is divided. It is a very important concept, because it is used for many things. One of the cases in which the denominator must be taken into account is when performing operations with fractions.
denominator examples
- 3/4: the denominator is 4, because it is the number of parts into which the unit is divided. This fraction means that from a unit, we make four parts and keep three.
- 2/3: the denominator is 3.
- 6/8: the denominator is 8.
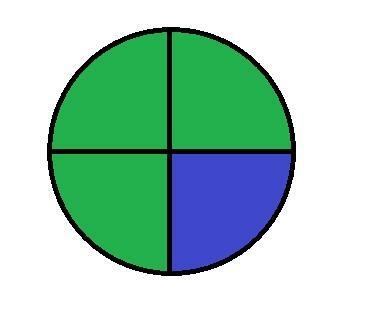
If we see it with a fraction in the image, we only have to look at how many parts the unit has been divided into, as in the following image:
As can be seen, the circle is divided into 4 pieces, with which we can determine that the denominator is 4.
As practical examples, we can name the slices of a pizza. That is, if we cut a pizza into eight pieces and eat two, the denominator would be 8, since it is the number of pieces we have made.
The common denominator involves changing several fractions so that their denominator is the same in all. To do this, a series of Steps which we will detail below:
- Write the denominators of the fractions to which we want to make the common denominator.
- Find the least common multiple of those numbers.
- Change the denominators of the initial fractions to the lowest common multiple.
- Change the initial numerators as follows: divide the least common multiple by the original denominator and multiply it by the original numerator. Repeat this process for each of the initial fractions.
Common denominator example
Let's see it with an example. The common denominator of the fractions 6/5 and 2/3 is found as follows:
- The denominators are 5 and 3.
- The least common multiple of 5 and 3 is 15.
- So, the initial fractions will be divided by 15: x/15 and x/15.
- We find the numerator by dividing 15 by the initial denominator and multiplying by the initial numerator, so for the first fraction, 15 divided by 5 is 3 and 3 multiplied by 6 is 18, so the first fraction will be 18/15. For the second fraction we follow the same logic: 15 divided by 3 is 5 and 5 times 2 is 10, so we are left with 10/15.
- In this way we already have our new fractions with a common denominator: 18/15 and 10/15.
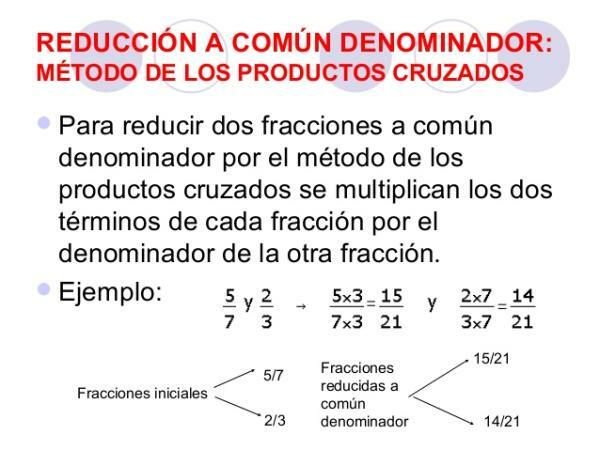
Image: The super owls
Now let's see if what has been explained throughout this lesson has been understood by means of the following exercises:
1. Identify the denominators of the following fractions:
- 5/2
- 9/7
- 12/24
2. Find the common denominator of 4/9 and 2/3

Check that you have done the proposed activities well:
1. Identify the denominators of the following fractions:
- 5/2: the denominator is 2.
- 9/7: the denominator is 7.
- 12/24: the denominator is 24.
2. Find the common denominator of 4/9 and 2/3
- The denominators are 9 and 3.
- The least common multiple of 9 and 3 is 9.
- So, the initial fractions will be divided by 9: x/9 and x/9.
- We find the numerator by dividing 9 by the initial denominator and multiplying by the numerator initial, so for the first fraction, 9 divided by 9 is 1 and 1 multiplied by 4 is 4, so the first fraction it will be 4/9. For the second fraction we follow the same logic: 9 divided by 3 is 3 and 3 times 2 is 6, so we are left with 6/9.
- In this way we already have our new fractions with a common denominator: 4/9 and 6/9.
If this lesson has helped you, remember that you can browse our website and find many more.



