Rule of multiples of 7 -Easy SUMMARY + EXAMPLES and VIDEO!

On this new occasion, from a PROFESSOR we are happy to present an always entertaining topic for lovers of mathematics: the multiples of 7 and their basic rules. For this reason, as we usually proceed in our lessons, we will present the concept of multiple or multiples from a general perspective. Then, accordingly, we will mention the relationship of this concept with the number 7 and finally we will present the properties of numbers that are multiples of 7. Read on and discover the rrule of multiples of 7!
Before knowing the rule of multiples of 7 it is important to review some concepts. As is our custom, in a TEACHER we like to review concepts that we have addressed in other articles but that are relevant, since they are part of the same lesson, applied to another context. Therefore, before entering the matter, it is important to remember what does it mean for a number to be a multiple of other.
When we speak of a multiple, we mean that a number contains another number a certain number of times exactly. In other words, a multiple number is when a
number is divisible to another exactly (that the result is a whole number).For example: we know that 6 is multiple of 3; because 6 contains 3 twice (6/3 = 2).
Thus, as based on the concepts of the previous section, we can affirm that the multiples of 7 are those that contain 7, an exact number of times. It is the same to say that everyone the multiples of 7 are divisible by 7 and its result will be an integer.
Some multiples of 7 are: 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168, 175, 182, 189, 196, 203, etc.
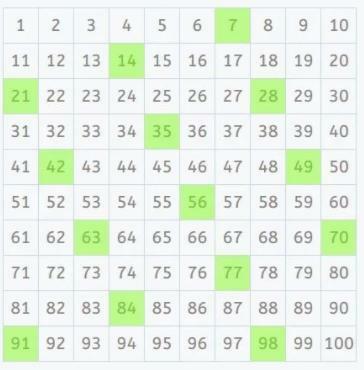
Image: Smartick
As you can already imagine, number 7 is quite particular, since it is a Prime number; that is, it is only divisible between 1 and itself. For this reason, it is more difficult to identify the multiples of the number 7 than with other numbers for examples the 2 or the 5 itself, that we have quite clear and simple rules to find the multiples of these numbers.
However, although there may be somewhat elaborate tricks to find a multiple of 7, the most reliable and safe is that of the Divisibility criteria. Which means that whenever a number is divisible by 7 (that the result of the division is a real and integer number), it means that we are in the presence of a multiple of the number 7.
However, there is a criterion that can help, together with what is described in the previous lines, to identify in which case it is a multiple of 7 or not. In the case of a 3 digit number we can apply this criterion or rule:
- We will separate the first two digits of the number in question
- Then we are going to subtract double from the remaining figure from that number, that is, from the figure that has remained by 2.
- If in the result of that operation, we obtain a multiple of 7, then the original number is a multiple of 7.
The next section will provide practical examples to understand this rule of multiples of 7.

Image: Slideshare
In a PROFESSOR we know that a good theory is always better accompanied by good examples that illustrate the concepts and facilitate the learning process. Based on this, we leave you some examples of what was commented in the previous section.
How to know if 119 is a multiple of 7?
11 - 9 x (2) = -7, and -7 is a multiple of 7. Therefore 119 is a multiple of 7.
How to know if 154 is a multiple of 7?
15 - 4 x (2) = 7, therefore 154 is a multiple of 7.
Now let's look at the case of 546
54 - 6 x (2) = 42, and 42 is divisible by 7, therefore 546 is a multiple of 7.




