REVERSE rule of three

On this occasion, from a teacher we are going to explain to you how to easily get a inverse rule of three. To begin with, we will remember what a rule of three is and, specifically, an inverse. Next, we will see how it is solved and some examples of rules of three inverses. To finish, we will propose a exercise and its solution.

Index

1. How to solve an inverse rule of three
2. Inverse rule of three examples
3. Inverse rule of three exercise
4. Exercise solution

The rule of three is the method for solve proportionality problems in which we know 3 values, but we must know a fourth, which is the unknown X.

In this way, we will find ourselves faced with problems in which there are two magnitudes, that is, things that can be measured. For each magnitude we will have to know a pair of data: two numerical for the first and one numerical and an unknown X for the second. To solve the problem that arises, the first thing we have to do is see if we are a relationship between direct or inverse magnitudes.

In this lesson, we are going to focus on the inverse, that is, that the two magnitudes of the problem they will have proportional variations in opposite directions: if one goes up, the other goes down; if one goes down, the other goes up; always in the same measure. That is, if one magnitude is multiplied by 2, the other will be divided by 2.

We'll see how we solve an inverse rule of three:

1. We order the magnitudes and their data
2. We assign an X to the data that we do not know
3. We multiply the data that are horizontally (side by side)
4. We divide the result by the data that we have not used

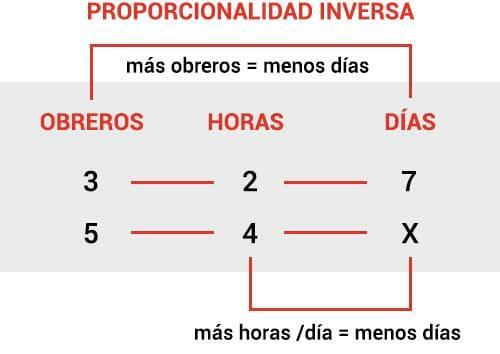
Image: Regladetres.net

The first thing to note is that we cannot confuse quantities with inverse proportionality with quantities with direct proportionality. Let's see some examples:

1. The days it takes to finish a work if we hire a certain number of laborers. They are inverse magnitudes, since if we hire more people, it takes less days, so if one magnitude goes up, the other goes down.
2. The hours it takes us to get home if we go at one speed or another. They are also inverse, since if we go faster, it will take less time.

Let's see some calculation example so it's clear how the rules of three inverses are solved:

• We have hired 4 people to fix a balcony that has fallen down and they have told us it will take 12 days. How many days would it take if we hired two more people?

The first thing we do is verify that they are inversely proportional magnitudes: when we increase the number of people who work, the days they have to work will decrease. Next, we order the data and assign an X to the unknown (to the data that we do not know):

Number of workers Days that take

4 12

6 X

To solve it, we multiply horizontally: 4 * 12 = 48; then we divide by the data that we had not used: 48/6 = 8. Thus, the answer is 8 days. It makes sense, because if there are 4 people working, it takes 12 days, but if there are 6 people working, it takes 8 days.

We are going to propose some activities to see if the mechanics of the rules of three inverses have been correctly understood.

1. If we drive at 120 km / h it takes us 2 hours to get home. How many hours will it take if we drive a little slower, at 100 km / h?
2. Check if these magnitudes are directly or inversely proportional: a) The cubes that a painter spends if he paints a certain number of pictures. b) The days it takes a painter to paint a picture and the days it takes two painters to paint the same picture.

Let's check if you have done the exercises correctly:

1.

We verify that these are inversely proportional magnitudes: when we slow down, the hours we take will increase. Next, we order the data and assign an X to the unknown (to the data that we do not know):

Speed ​​Hours it takes

120 2

100 X

To solve it, we multiply horizontally: 120 * 2 = 240; then we divide by the data that we had not used: 240/100 = 2.4. Thus, the answer is 2.4 hours.

2.

a) Directly proportional: if one goes up, the other goes up.

b) Inversely proportional: if one goes up, the other goes down.

If you want to read more articles similar to Inverse rule of three - with examples, we recommend that you enter our category of Arithmetic.