What is the THEATRAHEDRON and its characteristics

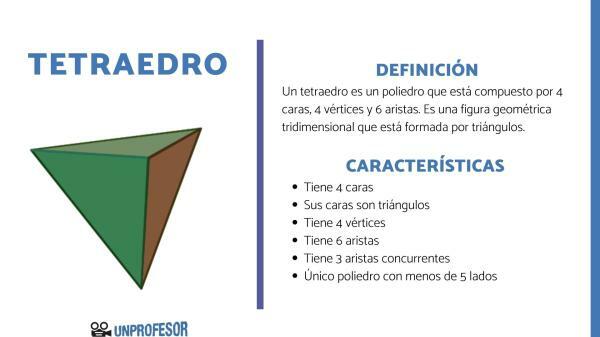
A tetrahedron is a polyhedron made up of 4 faces, 4 vertices, and 6 edges.; Furthermore, all the polygons that make up the tetrahedron are all triangles. In a new lesson from a Teacher we will see what is the tetrahedron and its characteristics. First we will start by reviewing what a polyhedron is, then we will see its types and we will end with the tetrahedron and its characteristics. Finally, the platonic solids and their elements.

A tetrahedron is a polyhedron which is composed of 4 faces, 4 vertices and 6 edges. It is a three-dimensional geometric figure that is made up of triangles. That is, the polygons that constitute the tetrahedron are all triangles.

The main characteristic of this polyhedron is that is the simplest of all, since it is the only one that has less than 5 sides. Tetrahedrons are pyramids that have triangular bases.

It has only four faces and therefore they are convex polyhedra, that is to say that the sides that connect to two of the points that form it are inside the polyhedron.

Taking into account that they are formed by triangles, we can say that at each vertex we find three of the faces that form it.

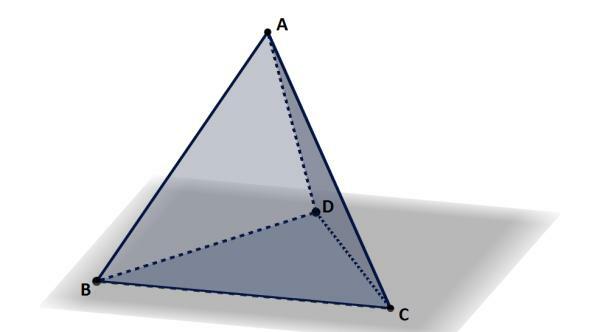
Now that you know what a tetrahedron is and its characteristics, we are going to review some basic concepts of geometry that will be very useful for you.

According to the geometry, we call polyhedra to the geometric bodies that They have volume, are three-dimensional, and have flat faces. They are geometric figures that occupy a part of the space and are delimited by different polygons.

• They are named according to the number of faces they have. In their name, the prefix they have determines that quantity, for example, pentahedrons, tetrahedrons, etc.
• Polyhedra are made up of faces, vertices, and edges.
• The edges are the lines that constitute the body of the polyhedra, and the points that join them are called vertices.
• The vertices of a polyhedron are the angles formed between three or more of its artists.
• The faces are those polygons that delimit them. They are flat and two-dimensional figures by which they are composed.

We can say that A tetrahedron is regular when the triangles that form it are all equal and equilateral. In other words, having all its faces the same, we can say that it is a regular polyhedron, just as each of its faces are also regular polygons.

Area of ​​a tetrahedron

To calculate the area of ​​a tetrahedron, you must add the area of ​​each of the triangles that form it. Being a polyhedron made up of triangles, we use the triangle area formula to calculate its faces, multiplying the base by the height and then dividing it by two.

A= (b x h) / 2

volume of a tetrahedron

To calculate the volume of the tetrahedron, the formula is used:

V = b x h x 1/3

In this formula, b is any of the faces of the polyhedron and h is the height that is generated from the union between b and the opposite vertex.

There are only 5 geometric bodies, called platonic solids, by the philosopher Plato, because they are regular and convex polyhedra in which all their faces are equal regular polygons, and the angles formed are also equal.

They are called perfect solids and have some similar characteristics What are they:

• their faces are regular polygons
• their angles are equal
• their edges have the same length
• the same number of edges and faces concur at their vertices

These solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.

1. tetrahedron: has four faces that are equilateral triangles, four vertices and six edges.
2. Cube: has six faces that are squares, eight vertices, and twelve edges.
3. Octahedron: has eight faces that are equilateral triangles, six vertices and twelve edges.
4. Dodecahedron: has twelve faces that are regular pentagons, twenty vertices and thirty edges.
5. icosahedron: has twenty faces that are equilateral triangles, twelve vertices and thirty edges.

These regular polyhedra are called Platonic, not only because of "Plato" but also because he associated each polyhedron with one of the four elements, air, water, fire and earth, and the last one with the Universe itself same.

The tetrahedron was associated with fire, the octahedron with air, the icosahedron with water, the cube with earth, and the dodecahedron with the Universe.