How to calculate the AREA of an octahedron
To calculate the area of an octahedron we must make the sum of the surfaces of the eight faces that has. In unProfesor we discover the formula and examples so that you understand it better. An octahedron is a three-dimensional geometric figure which is made up of eight polygons. It is a polyhedron that can be regular or irregular but always has eight faces that can be the same or not. Depending on this, the area of an octahedron may or may not be calculated.
In a new lesson from a Teacher we are going to work how to calculate the area of an octahedron. We will start with the concept of the octahedron, then we will continue with the elements that make up the octahedron. We will continue with the calculation of the area to end with some exercises.
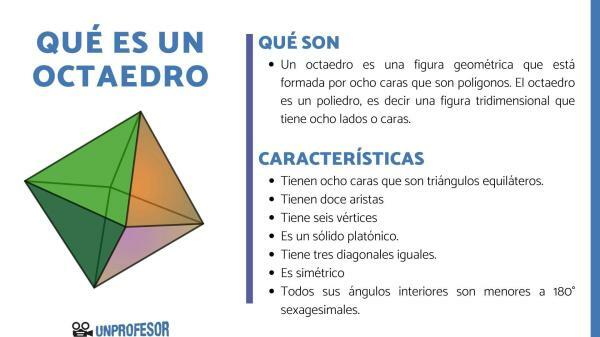
In geometry, a octahedron is that one three-dimensional figure with eight faces in which each of them is a polygon.
An octahedron is a polyhedron. Remember that a polyhedron is a three-dimensional geometric figure that is formed by different faces that are polygons. While a polygon is a two-dimensional geometric figure that is built from line segments that are joined to form a place or space of the closed plane.
The faces or sides of an octahedron, that is, the polygons that form it, can be triangles, squares, pentagons, hexagons and heptagons, that is, any polygon that has less than eight sides or segments of straight.
Characteristics of an octahedron
Octahedrons can be regular, and this is because they are made up of eight triangles that are equilateral, that is, all the sides of the polygon are equal. The regular octahedron is seen as the union of two pyramids from their bases. Therefore it has eight faces, it has twelve edges and six vertices. This type of octahedron is called a Platonic solid. There are five bodies considered within this group and they are the cube, tetrahedron, octahedron, dodecahedron and icosahedron.
The main characteristic of these Platonic solids is that are regular polyhedra and convex. That is to say, that they are formed by polygons that are all regular or equal to each other, and that we can always join two points with a line inside the polyhedron.
the octahedrons irregular are those polyhedra that have eight faces but they are NOT the same to each other and do not have equal angles. The number of faces an irregular octahedron has can vary, but the number will always be an EVEN number.
As a characteristic, an octahedron that is irregular always has eight vertices and twelve edges. That is to say, like any octahedron, apart from having eight faces as its name indicates.
To find out how many faces one of these polyhedra has, we can only count them. It depends not only on the shape of the polygons that form it, but also on the size of each one of them.
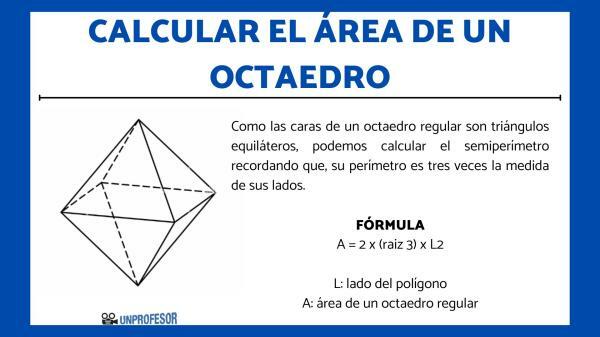
To calculate the area of an octahedron, we must calculate the sum of the surfaces of the eight faces that has. Therefore, we can calculate the area of an octahedron that is regular by equaling the square of the edge of an octahedron by two times the root of the number three.
As the faces of a regular octahedron are equilateral triangles, we can calculate the semiperimeter remembering that its perimeter is three times the measure of its sides. The octahedron area formula then, it is as follows:
A = 2 x (root 3) x L2
- L: side of the polygon
- A: area of a regular octahedron
examples
We want to calculate the area of an octahedron whose edge measures 15 m.
We start then. Each side of the polygon measures 15 m. So:
- A = 2 x (root 3) x L2
- A= 2 x (root 3) x 152
- A = 779.42 m2
Therefore the area of an octahedron with edge 15 cm is equal to 779.42 m2

To conclude this lesson on how to calculate the area of an octahedron, we are going to leave you some exercises with solutions so you can practice at home.
- Calculate the area of an octahedron with an edge of 5 cm.
- Calculate the area of an octahedron with an edge of 76 cm.
Solutions
- Each edge measures 5 cm, therefore L= 5 cm
- A = 2 x (root 3) x L2
- A= 2 x (root 3) x 52
- H = 86.6cm2
Therefore the area of an octahedron of edge 5 cm is equal to 86.6 cm2
2- Each edge measures 76 cm, therefore L= 76 cm
- A = 2 x (root 3) x L2
- A= 2 x (root 3) x 762
- W = 69312 cm2
Therefore the area of an octahedron with edge 76 cm is equal to 69312 cm2
If you liked this lesson, share it with your classmates. And remember that you can continue browsing the page. On the website of a Teacher there is very interesting content that can be useful to you.