How to calculate the AREA of an ISOSCELES triangle
In a Professor we are going to deal with a topic that is of utmost importance for your training in the area of mathematics and, in particular, in the field of geometry. For this reason, in this lesson we are going to introduce you, first, the general concept of the area in geometry, in the second section we are going to talk about the basic components of a isosceles triangle. In this sense, we will enter into the matter, since in the third section we will explain how to calculate the area of an isosceles triangle and, finally, in the last section we are going to provide you with a example so that you can apply what is exposed in the theoretical paragraphs about the area in geometry.
Index
- How do you find the area of a triangle?
- What is an isosceles triangle?
- How to find the area of an isosceles triangle?
- Exercise to find the area of an isosceles triangle
How do you find the area of a triangle?
In the realm of geometry, it is known as
area the measure of surface that a given figure occupies in space; that is, it is the inner region that forms a figure specifically within the space. Also, the area of a figure is used in many important professions that apply geometry to their functions; These can be professions such as engineering, architecture, or even graphic design.In this sense, it is also important to comment that having a correct perception of what an area represents will be useful. for many daily activities that you carry out on a day-to-day basis, whether at home, at school, work and other types of activities.
It is important to remember that, once the area of a figure has been calculated, this quantity must be represented in units of measure squared. This means that the area is written, for example, in centimeters squared (cm2), meters squared (m2), etc.
With this, in the next section we will explain the concept of the isosceles triangle and its basic components. In the third section we are going to continue, joining both contents, to explain how the area of an isosceles triangle is calculated.
What is an isosceles triangle?
The basic concept of a isosceles triangle is that it is composed of two sides and two equal angles. What would be called the base is the side that is different from the other two sides. That they are the same means that they have The same size; in other words, they are the same length or measure.
Also, to broaden the term, the two equal sides are called legs -the term isosceles comes from the union of two Greek words: «isos "(equal) and"skelos »(leg) - and the uneven side is called base.
We can add that this type of triangles is one of the most famous within the area of geometry and therefore, This lesson is of great interest, since you will surely see it throughout your academic life within the field scientific.
Now, in the next section we are going to focus on explaining how to get the area of a isosceles triangle and we will leave you an example so that you can visualize the explanation in a more effective.
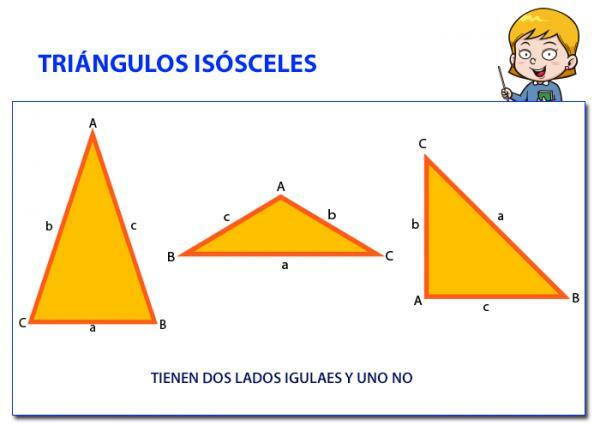
Image: Primary World
How to find the area of an isosceles triangle?
As we have mentioned in previous lines, in this section we are going to explain how to find the area of an isosceles triangle. Also, you already know that the area is calculated by a specific formula depending on the figure in question. In this case, it is the isosceles triangle and like every triangle it has a certain formula to know its area.
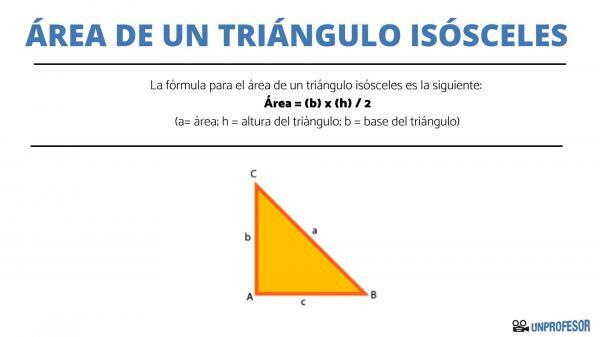
This is how the formula to know the area of a triangle is:
A = (b x h) / 2
Where: A = Area; b = base; h = height
This formula is always taking into account that within the proposed exercise they provide you with all the data of the formula and simply substitute the figures within the formula and calculate it. In more advanced levels of this topic, you will have to obtain some data with mathematical operations and geometric, but for now what you have to take into account is the use and application of the formula for the triangle.
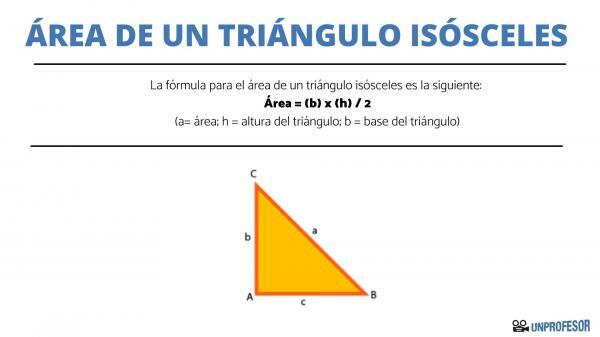
It is very important to mention that the height corresponds to the distance that exists between the vertex of the different angle and the midpoint of the line that represents the base of the triangle. So that you can appreciate it better, we leave you an image so that you can visualize which line represents the height in an isosceles triangle.
Exercise to calculate the area of an isosceles triangle.
As an example we can carry out a brief exercise so that you can appreciate what is explained in the theoretical section.
Example: Isosceles triangle with height 15 cm and base of 8 cm
- A = b x h / 2
- A = 8 x 15/2 = 60 cm2
NoteRemember that you must express the resulting quantity in units of measurement squared.
To end the lesson, as is customary from our unProfesor portal, we encourage you to continue your training and put all your efforts into your academic activity. For any questions, you know that you can count on the content of this type of topic on our website, since we are here to help you in your training.
Go ahead and cheer up!
If you want to read more articles similar to How to Find the Area of an Isosceles Triangle, we recommend that you enter our category of Geometry.