Parts of a MONOMIUM

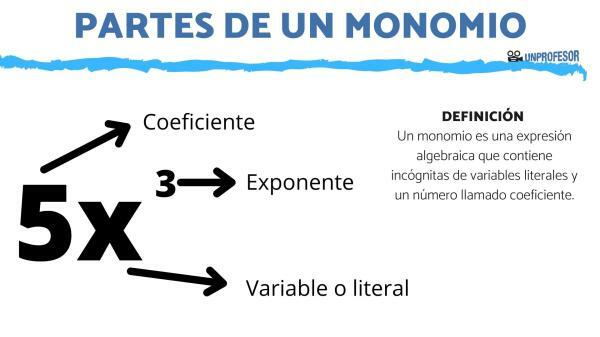
From unProfesor we bring you a new math lesson that will be very useful, especially in the study of a branch of mathematics called algebra. Specifically, we are going to see the parts of a monomial, so first we will clarify what a monomial is and, in the end, we will propose a resolved exercise so that you can verify that you have acquired the explained knowledge.

A monomial is that algebraic expression that contains literal variable unknowns (i.e. letters) and a number called coefficient. These monomials only have one term, since if there were one addition or a subtraction would be called a binomial.

So, as additions or subtractions cannot appear, since then it is not considered a monomial, can there be multiplications and powers? The answer is yes, as long as the power number is a natural number.

On the other hand, if there are several monomials adding or subtracting, we have a polynomial.

We'll see examples of each of the parts of a monomial, so that it is better understood what each of them means:

1. If we have the monomial 6x²:

• The coefficient is 6.
• The literal part is x.
• The individual degree is 2 and the absolute as well.

2. If we have the monomial 5x²and³:

• The coefficient is 5.
• The literal part is xy.
• The individual degree of x is 2 and that of y is 3. The absolute degree is 5, because 2 + 3 = 5.

3. If we have the monomial 93xy⁴z:

• The coefficient is 93.
• The literal part is xyz.
• The individual degree of x is 1, that of y is 4, and that of z is 1. The absolute degree is 6, since 1 + 4 + 1 = 6.

4. If we have the monomial -x:

• The coefficient is -1.
• The literal part is x.
• The individual degree is 1, the same as the absolute.

5. If we have the monomial xy:

• The coefficient is 1.
• The literal part is xy.
• The degree of x is 1 and the degree of y is 1. The absolute degree is 2, because 1 + 1 = 2.

To check that you have understood what has been explained throughout this lesson on monomials, we recommend that you do the proposed exercises:

1. Indicate which are the parts of the following monomials:

• x⁴
• 89x⁶and²

2. Calculate the individual degree and the absolute degree of the following monomials:

• -2x²and Z
• 8x

Then we leave you the answer to the activities raised above, so you can check if you have done them correctly:

1. Indicate which are the parts of the following monomials:

• x⁴: the coefficient is 1, the literal part is x and the degree is 4, both individual and absolute.
• 89x⁶and²: the coefficient is 89, the literal part is xy and the degree is 6 for x and 2 for y, although the absolute is 8.

2. Calculate the individual degree and the absolute degree of the following monomials:

• -2x²yz: The individual degree is 2 for x, 1 for y, and 1 for z. The absolute degree is 4.
• 8x: the individual degree is 1, the same as the absolute.

If you liked today's lesson, remember that you can share it with your classmates and you can continue browsing our tabs to read more interesting lessons.