What are HETEROGENEOUS monomials

In this new lesson from a Teacher we are going to study the Heterogeneous monomials and examples, which will help you to study the branch of mathematics known as algebra. In this way, we will start studying the description of a monomial and its parts and, later, we will know what a heterogeneous monomial is. We will also see examples and, at the end, you will be able to find resolved exercises to check that you have understood what we have explained in this lesson.

Index

1. what is a monomial
2. What are heterogeneous monomials
3. Examples of heterogeneous monomials
4. Heterogeneous monomials exercise
5. Solution

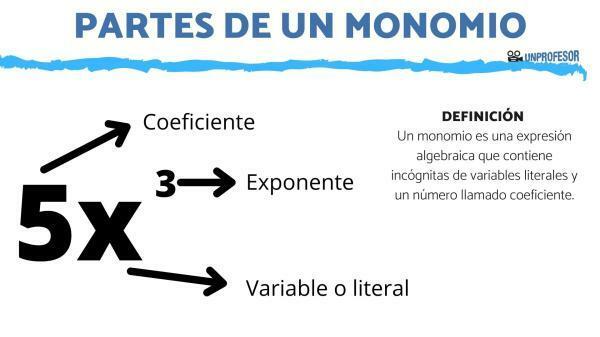
The monomials are those algebraic expressions that contain unknowns of literal variables (that is, letters) and a number that we know as a coefficient. Monomials only have one term, since if we were to find an addition or a subtraction it would no longer be a monomial, but a binomial.

In any case, despite the fact that neither addition nor subtraction appear, we can find

The parts of a monomial There are basically three:

• The literal part, which are the letters of the monomial.
• The coefficient, which is the number that multiplies the literal part.
• The degree, which is the sum of the exponents of all the letters.

What interests us most in this lesson is to understand well what the degrees of monomials are.

Let's see what interests us in this lesson: what are heterogeneous monomials.

For two monomials to be considered heterogeneous we have to see that its absolute degree is different, that is, if we add all the exponents of each of the letters of the literal part, the number we get is not the same in the monomials we are studying.

It is also important to emphasize that the exponents they will only be natural numbers from one, that is, if one of the exponents is zero, that letter will simply not appear. On the other hand, it is necessary to emphasize that if we see a letter without an exponent, what we are actually seeing is an exponent of 1.

Image: Youtube

Let's see some examples of heterogeneous monomials to understand it better:

• The degree of the monomial 3x²and⁴ is 6, since 2 + 4 = 6.
• The degree of the monomial 6x²and⁵ is 7, since 2 + 5 = 7.
• Therefore, these monomials are heterogeneous.

The literal part doesn't have to be the same, so we just have to look at the degree. For example:

• The degree of monomial 4q³r⁴ is 7, since 3 + 4 = 7.
• The degree of the monomial 9yz⁵ is 7, since 1 + 5 = 6.
• Therefore, these monomials are heterogeneous.

Definitely, we have to add the exponents of each of the letters. We can have whatever letters they are, they don't have to be 1 or 2.

Let us now practice what we have been learning throughout the lesson with the activities that we now propose:

1. Specify the degree of the following monomials:

• 40xy⁷
• 2s³you³
• 7m⁶n⁴

2. Justify if the following monomials are heterogeneous or not:

• 6x³and; 2x²
• 90x³z; 8x²z²
• 25cu; 32cu

We are now going to check that what has been explained has been understood by looking at the solutions to the proposed activities:

1. Specify the degree of the following monomials:

• 40xy⁷: since 1 + 7 is 8, the degree of this monomial is 8.
• 2s³you³: since 3 + 3 is 6, the degree of this monomial is 6.
• 7m⁶n⁴: Since 6 + 4 is 10, the degree of this monomial is 10.

2. Justify if the following monomials are heterogeneous or not:

• 6x³and; 2x²: the first monomial has degree 4, because 3 + 1 is 4; the second is of degree 2, because it only has one letter and this one has an exponent of 2. In this way, they are heterogeneous monomials, since their degrees are different.
• 90x³z; 8x²z²: the first monomial has degree 4, because 3 + 1 is 4; the second is of degree 4, because 2 + 2 is 4, so we can confirm that these monomials are not heterogeneous.
• 25cu; 32cu: the first monomial has degree 2, since 1 + 1 is 2; the second is of degree 2 as well, because 1 + 1 is 2. In this way, they are not heterogeneous, although we could already see it with the naked eye: when two monomials have exactly the same literal part, they will never be heterogeneous.

If you want to read more articles similar to Heterogeneous monomials - with examples, we recommend that you enter our category of Algebra.