What are the VERTICES of a triangle?
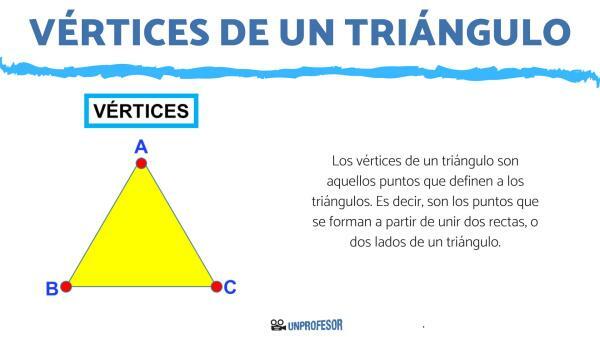
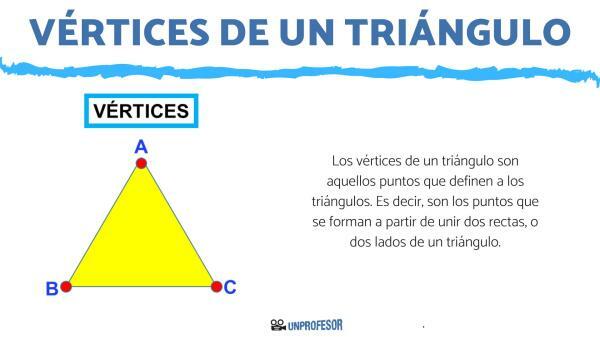
The vertices of a triangle are those points that define the triangles and there are always three In a new lesson from a Teacher we will describe in more depth what are the vertices of a triangle. We will begin by reviewing the concept of a triangle along with its elements. Then we will see the equality of triangles together with their criteria, and finally we will talk about a theorem related to vertices. To consolidate what we have seen, we will exercise with a true and false about the triangles.
Let's review the concept of triangle. the triangles are flat and basic geometric figures formed by three sides that are in contact with each other, from common points that unite them called vertices.
The word triangle is because these basic plane figures have three interior angles that are formed by each pair of lines that are in contact at the same vertex.
The elements of a triangle are:
- sides: straight lines that form the triangle, and join the vertices. These lines delimit the figure and always have only three sides.
- angles: Two sides of a triangle form an angle at the common vertex. This angle is called the interior angle of the triangle. Triangles have only three interior angles.
- And finally the vertices of a triangle.

The vertices of a triangle are those points that define the triangles. That is, they are the points that are formed from joining two lines, or two sides of a triangle.
In triangles there are ALWAYS only three vertices.
In mathematics a midpoint means that it is the point that is the same distance of two other points whatever these may be. They are also called equidistant points.
If we talk about a segment, the midpoint or equidistant is the point that divides the segment into two equal parts.
Triangles have three midpoints, and are those that are located in the middle of each segment and have the same distance from there to the vertices that form each side.
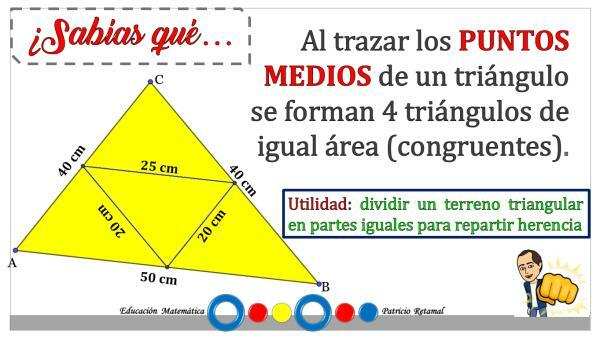
Image: Teacher of Teachers
People say that two triangles are congruent if, by some movement, we can make them coincide. That is, if they have the same sides and the same angles. Coincident sides are called corresponding or homologous.
We can say, in other words, that two triangles are congruent if their corresponding sides have the same length and the corresponding angles have the same measure or width.
There are certain criteria for the congruence of triangles and these are:
One equal side and two adjacent angles or angle, side, angle criterion
Two triangles are congruent if they have two corresponding angles and the side included between them corresponding.
Two equal sides and the angle between them or criterion side, angle, side
Two triangles are congruent if they have two corresponding sides and the angle between them congruent.
Three equal sides or side, side, side criterion
Two triangles are congruent if their corresponding sides are congruent.
The congruence of the triangles can be easily measured since we only need three measurements. Since we can divide any polygon into triangles, this is a very powerful tool for working with the congruence of much more complex shapes.
Why side, side, angle is not a criterion of congruence of triangles?
Two pairs of corresponding sides and one pair of corresponding angles are not necessarily congruent, that is, they can be congruent but not always.
With this criterion there is usually not enough information when the corresponding angles are opposite the lesser of the two known sides in the triangle.
If by the vertices of a triangle are drawn parallel to the opposite sides, then another triangle is obtained such that the midpoints of its sides are the vertices of the die.
The triangle formed is called anticomplementary of the previous
The vertices of a triangle are the segments that form it.
Fake. The vertices are the points that join the segments called sides, which delimit the figure.
Two triangles are congruent if they have the same sides and the same angles.
TRUE. They are congruent if their corresponding sides have the same length and the corresponding angles have the same width.
Triangle ABC of sides 7 cm, 4 cm, and 3 cm is congruent to triangle DEF of sides 3 cm, 4 cm, and 8 cm.
Fake. With the criterion side, side, side we can see that the three sides do not have the same length, therefore the triangles ABC and DEF are not congruent.
Triangle ABC with angle 30° side 5 cm and angle 45° is congruent with triangle DEF with angle 45° side 5 cm and angle 30°.
TRUE. With the criterion angle, side, angle we can see that the two angles adjacent to the informed side have the same measure, just as that side has the same length.
Triangles are flat geometric figures formed by four segments.
Fake. Triangles are figures formed by three sides that are in contact with each other through the vertices.
Triangle ABC of side 3 cm, angle 35° and side 4 cm is congruent with triangle DEF of sides 4 cm and 3 cm and the angle formed between them measures 35°.
TRUE. According to the criterion side, angle, side the two triangles have the same length of sides and the angle formed between them has the same width, therefore they are congruent.
If you liked this lesson from a Teacher, don't forget to share it with your classmates. You can continue browsing the web to find more content like this.