Extract the AREA of an EQUILATERAL triangle

Once again, from a Teacher we bring you a new lesson, this time explaining how to find the area of ​​an equilateral triangle, basic knowledge for the study of the geometry. To begin, we will review the concepts of triangle and equilateral. After that, we will clarify what the area is and how to calculate it in this particular polygon. Finally, we will propose a exercise with its posterior solution, to fix what has been learned.

A triangle It is that polygon that has three edges or sides, three vertices and three angles. From this definition it follows that they can be figures of different types, since they can have sides of different lengths or angles of different amplitudes.

This is where the word comes into play equilateral, as it means that a equilateral triangle have all sides equal and all angles equal. In this sense, as the sum of the angles of a triangle always gives 180º, in an equilateral triangle each angle will measure 60º obligatorily.

The area is the calculation that allows us to find out

how much space does it occupy a figure. Therefore, the area of ​​an equilateral triangle will quantify how much surface area that triangle occupies. It is worth mentioning that the area is always resolved in squared units, so that, if they provide us with the data in centimeters, the area will turn out to be in centimeters squared. The same if they provide us with the statement in meters, since the area will be in meters squared.

It is also very important to remember that, in order to calculate the area of ​​any polygon, it is necessary that the units coincide; that is, if one side of the figure is in meters and the other in kilometers, we will have to unify those measurements to be able to calculate the area. Either we change the meters to kilometers or we do the opposite, but it is mandatory that we have the same units.

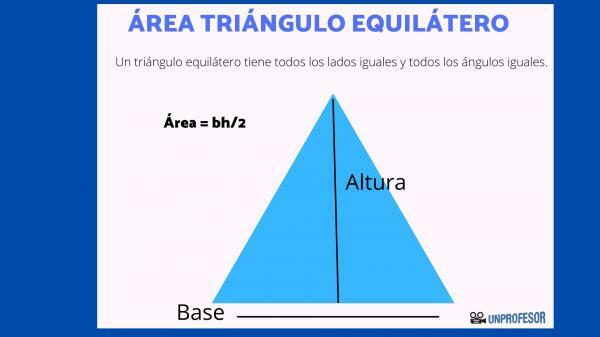
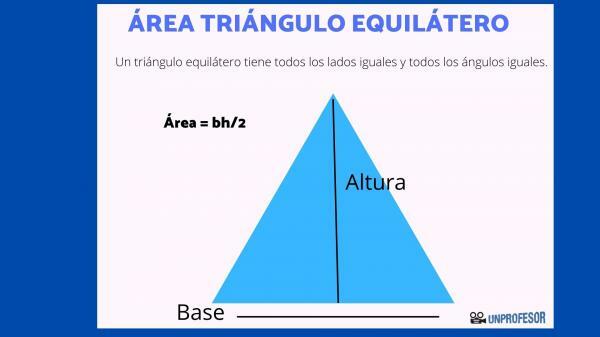
Once all this is clear, we can proceed to calculate the area of ​​an equilateral triangle. The formula is the next:

• Area = (b x h) / 2
• Where b = base; h = height.

In short, we simply have to multiply the base of the triangle by the height, which is the line that crosses from the vertex to the base, and then divide by 2. Perhaps the most complicated thing is to find the height, since they will not always provide it to us in the statement directly.

In order to find the height of an equilateral triangle, we must apply the Pythagoras theorem, which you can consult in the link that you have right in its name. So, since the three sides of an equilateral triangle are equal, we split the triangle in half, that is that is, from the vertex to the base, and we already have two right triangles to be able to apply the Theorem. The height will be one leg, half side will be the other leg, and the full side will be the hypotenuse.

Another way of find the height less intuitive and more memoristic, but that serves the same way is the one that results from applying the formula: (base x root of 3) / 2

Let's see if you've got solve the exercises correctly raised:

• In the first section they give us the base and the height, so we simply have to multiply both and divide by 2: (3 x 2.6) / 2 = 3.9 centimeters squared = 3.9 cm².
• In the second section they do not give us the height, so we must find it using the Pythagorean Theorem. So, we will use the hypotenuse formula² = leg² + leg², applying the numbers: 5² = 2,5² + height². We solve: 25 - 6.25 = height²; 18.75 = height²; we take the square root of the number and we have that the height is 4.33 cm². Now we can calculate the area: (5 x 4.33) / 2 = 10.825 cm².

If you want to read more articles similar to this, we recommend that you enter our category of Geometry and, specifically, in the section on Perimeters and areas.