ANGLES classification according to their sides

From a PROFESSOR we are pleased to present this time an extension of a topic that is essential for the area of ​​geometry: the classification of angles according to their sides. In this topic we will see how line segments form an angle when they intersect in space. As we usually proceed, we will start by defining the concept of angle and then list the different types of angles according to their sides, or what is the same according to the interception of said lines.

It should be mentioned that this topic is deeply related to the topic of triangles, since some names within the classification of angles coincide with the different types of triangles, since these angles are part of that triangle. It's a fundamental subject within geometry and understanding it in its entirety is of utmost importance for topics that we will see in the future in a PROFESSOR within geometry.

Although we have already given a hint of what an angle means, it is always very important to define it theoretically.

In this sense, we can say that a

angleit's a geometric concept that refers to the space that exists between the intersection that part or are in the same point, called vertex. The angle will always be measured in degrees. Other texts define the angle as a portion of the plane between two rays that have a common origin.

In any case, the fundamental thing is to understand that the angle is formed by the intersection of two straight lines. Precisely that space between the two mentioned lines is what we know as an angle.

Now, we remind you that in this lesson we will base ourselves solely and exclusively on the types of the angles according to their sides, since there are other classifications and it can generate some confusion.

This is how once the concept of angle is exposed, we can move on to the angle classification according to their sides, since it is extensive and very interesting. Here you have it:

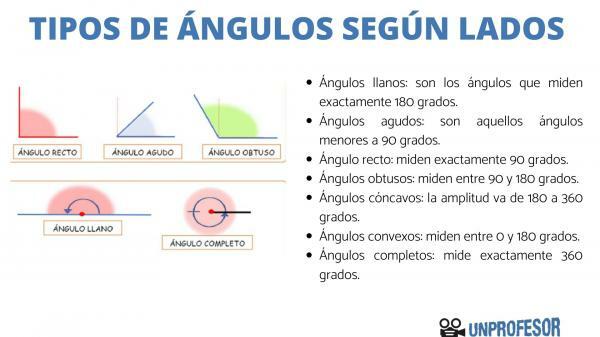
• Flat angles: are the angles that measure exactly 180 degrees. At first glance, the graphical representation of this angle is a straight line, since the intersection of the two lines in question cannot be seen.
• Acute angles: are those angles less than 90 degrees. That is, its amplitude does not exceed 90 degrees, the lines in this case would be at a shorter distance.
• Right angle: perhaps the easiest to memorize, because they are the angles that measure exactly 90 degrees. In other words, the lines are completely perpendicular to each other.
• Obtuse angles: These angles are those that measure between 90 and 180 degrees. Which means that your measurement is greater than 90 but less than 180 degrees.
• Concave angles: Refers to angles whose amplitude ranges from 180 to 360 degrees. The measure of these angles is greater than 180 but less than 360 degrees.
• Convex angles: are those angles that measure between 0 and 180 degrees. Its amplitude is greater than 0 but less than 180 degrees.
• Full angles- A full angle is one that measures exactly 360 degrees. The visual representation of this angle is a circle.

As we have mentioned in previous lines, this topic is essential for a successful start within the world of geometry; since later we will see that there are other types of angles such as negative angles, angles according to their position, according to their sum, complementary angles, etc. So from a PROFESSOR we encourage you to study these elementary concepts to arrive with strength and prepared for future lessons within the geometric field.