What are the DIVIDERS of a number
From a PROFESSOR we present you a new math lesson on the divisors of a number, an important concept for the knowledge of divisibility in arithmetic. First of all, as always, we will start by defining what divisors are and see how is the best way to find them. Next, we will see several examples. Finally, we will do a exercise and we will leave you the solution so that you can check that you have understood it correctly.
Index
- What are dividers?
- Steps to find the divisors of a number
- Examples of the divisors of a number
- Divisor Exercise
- Solution
What are dividers?
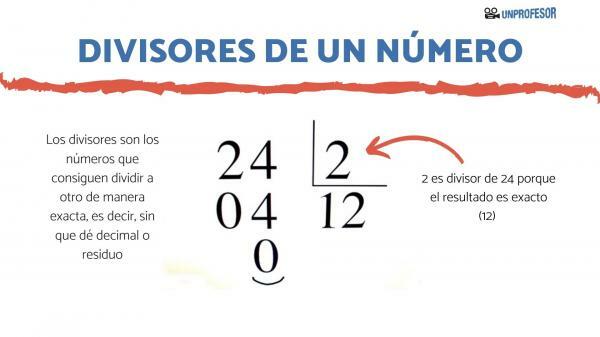
The divisors are the numbers that get divide another exactly, that is, without giving a decimal or remainder. Another way of looking at it is that one number is a divisor of another if it is included in the latter a certain number of times.
The easiest way to see it is with objects from everyday life that cannot be broken into pieces like, for example, with pencils. In this way, to find the dividers, we only have to see how many pencils we can put in each group if we decide to distribute them into cases.
Steps to find the divisors of a number.
In order to calculate the divisors of a numberand not forgetting any of them, it is best to do it as follows:
- We write D (number for which we are looking for divisors) = {1, ________________, number for which we are looking for divisors}, leaving a good space in the middle.
- We start dividing that number by 2 and, if it is accurate, we point the 2 to the right side of the 1 in the previous step and the quotient of the division on the left side of the number from which we look for the divisors within the brackets.
- We do the same with 3, 4, 5... like this until we get to divide by the last number that we have found to the right in the brackets.
Examples of the divisors of a number.
We will understand all this better with a calculation example. If we were asked to find the divisors of 32, we would follow the previous steps:
1. We write D (32) = {1, ______________, 32}, remembering to leave a space in the middle of both numbers inside the brackets.
2. We divide 32 by 2 and it gives us exactly 16, so we put it inside the brackets as explained in step 2: D (32) = {1, 2, ______________ 16, 32}
3. We divide by 3 and we see that it is not exact, so we do not write it down. We divide by 4 and it gives us 8, so we add it to the brackets: D (32) = {1, 2, 4, __________ 8, 16, 32}. We divide by 5 and it does not give exact. Nor between 6 and 7. The next number that we should divide by is 8, but it is already the one we had on the right in the brackets, so this means that we have finished looking for the divisors and, for that reason, we can now eliminate the space in the center: D (32) = {1, 2, 4, 8, 16, 32}.
Other examples of dividers can be:
- D (1) = {1}
- D (2) = {1,2}
- D (3) = {1,3}
- D (4) = {1,2,4}
- D (5) = {1,5}
- D (6) = {1,2,3,6}
- D (7) = {1,7}
- D (8) = {1,2,4,8}
- D (9) = {1,3,9}
- D (10) = {1,2,5,10}
- D (11) = {1,11}
- D (12) = {1,2,3,4,6,12}
- D (13) = {1,13}
- D (14) = {1,2,7,14}
- D (15) = {1,3,5,15}
- ...
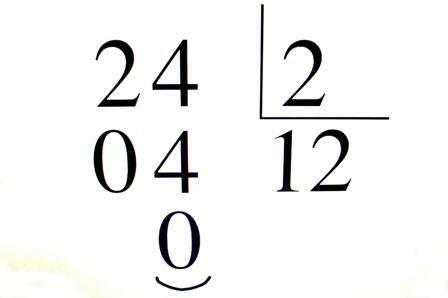
Divisor exercise.
To see if you have correctly understood the theory that we are explaining to you today, we propose a series of divisor exercises:
- Find all the divisors of 68.
- Is 90 a divisor of 1170? Justify your answer.
- In how many different ways can I group a class that has 30 students? Specify how many students each group would be.
Solution.
Let's now look at the solutions:
1. D (68) = {1, 2, 4, 17, 34, 68}.
2. Since 1170 can be divided by 90 and it gives 13 without a remainder, that is, it gives exact 13, then we can say that 90 is a divisor of 1170.
3. First, we must find the divisors of 30, which are: D (30) = {1,2,3,5,6,10,15,30}. So we see that it has 8 divisors in total, so I can group the students in 8 different ways:
- 1 group of 30
- 2 groups of 15
- 3 groups of 10
- 5 groups of 6
- 6 groups of 5
- 10 groups of 3
- 15 groups of 2
- 30 groups of 1
We hope that this lesson has been helpful to you and that you have been able to understand all the concepts that have been explained. If you want to investigate more in the area of divisibility within mathematics, you can navigate through the corresponding tab: Divisibility, within the Arithmetic section.
If you want to read more articles similar to What are the divisors of a number - with examples, we recommend that you enter our category of Arithmetic.



