What is a MATRIX in mathematics
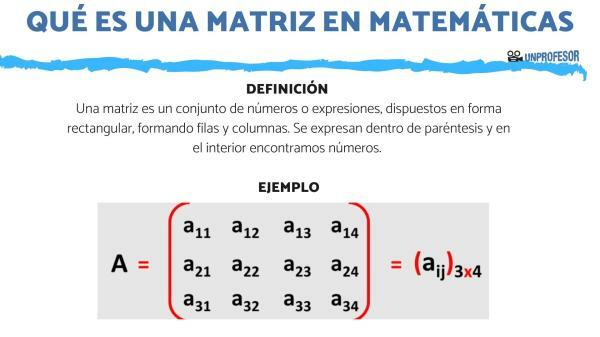
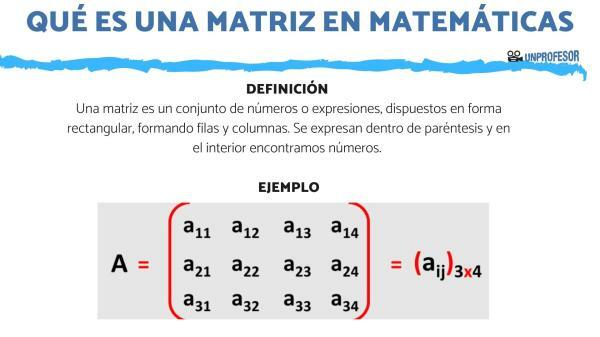
In a Teacher we are going to explain thatWhat is a matrix and examples. The matrix is a set of numbers or expressions, arranged in a rectangular shape, forming rows and columns. They are expressed within parentheses and inside we find numbers, mostly. He guy of matrix, is expressed as the number of rows times the number of columns. For example: 3x3 matrix.
Each number that exists inside the matrix can be expressed and called according to your position inside the matrix, as follows: Xij; “i” as the number of the row in which the number is located; “j” as the number of the column in which the number is found. Below we will tell you and leave you exercises with solutions so you can practice at home.
Index
- What is a matrix?
- Types of arrays
- How to make a matrix?
- What is a scalar matrix and example?
- What are matrices for?
- Matrices: exercises with solutions
- Solutions
What is a matrix?
A matrix is a set of numbers or expressions, arranged in a rectangular shape, forming rows and columns. They are expressed within parentheses and inside we find numbers, mostly.
Each number that exists inside the matrix can be expressed and named according to its position within the matrix, as follows: Xij
- “i” as the number of the row in which the number is located
- “j” as the number of the column in which the number is found.

Types of matrices.
exist different types of matrices, as we will see below:
- row matrix- It only has one row, regardless of how many columns it has.
- Column matrix- It only has one column, regardless of how many rows it has.
- Square matrix: It is that matrix that has the same rows as columns, so it has a diagonal.
- rectangular array: it has a different number of rows than columns, so its dimension is expressed as mxn.
- Null matrix: It is that matrix in which all elements are zero.
- Upper triangular array: It is that matrix in which the elements that are below the diagonal are zeros.
- Lower triangular array: is that matrix in which the elements that are above the diagonal are zeros.
- Diagonal matrix: is the matrix that only has non-zero elements on the diagonal. That is, the elements above and below the diagonal are zeros.
- Scalar matrix: It is one in which the elements of the diagonal are identical.
- identity matrix: all its elements are zeros, except the diagonal, which are ones.

How to make a matrix?
To create a matrix, we must be clear how many rows and how many columns Will have.
From there, we put two large parentheses and inside we write each of the elements. In this way, the matrix can be 2x1, 3x4... Any combination that occurs to us will be valid.
Inside the matrix, The elements can be both positive and negative. They can also be zeros.
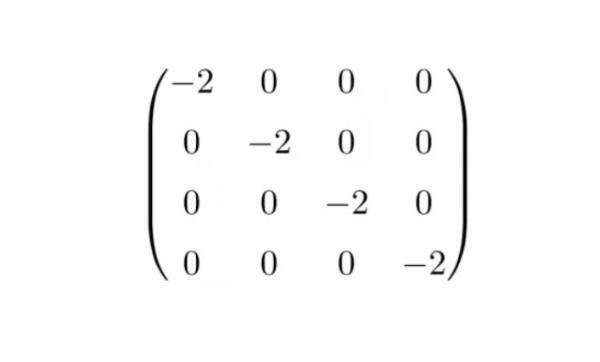
What is a scalar matrix and example?
The scalar matrix is one in which the elements of the diagonal are identical, as in the example in the attached image.
This type of matrix is, in turn, a diagonal matrix, so They are always symmetric matrices. They are, at the same time, an upper triangular matrix and a lower triangular matrix.
The identity matrix explained in the paragraph on types of matrices is a scalar matrix and We can obtain any scalar matrix from the product of an identity matrix and a number climb.
What are matrices used for?
Matrices have many and varied applications, since they are very useful.
For example, the matrices are used for:
- Animate objects and shapes in computer graphics
- To program bionic arms,
- Solve systems of equations in mathematics…
- They are also widely used to obtain statistics, for example to calculate parameter estimates in a multiple regression model.
Also, here you have more solved matrix exercises.
Matrices: exercises with solutions.
To check if you have understood what has been explained in today's lesson, we recommend that you Do the following exercises:
1. Justify if it is true or false:
- An identity matrix is a scalar matrix.
- The matrices are always square.
- A matrix can exist with only one row.
Solutions.
Then you can find out If you have correctly carried out the proposed activities:
1. Justify if it is true or false:
- An identity matrix is a scalar matrix: this is true, since the identity matrix has a diagonal made up of ones and the scalar matrix implies that all the numbers on the diagonal are the same, so an identity matrix will always be a scalar, but a scalar matrix will not always be an identity.
- Matrices are always square: this is false, since they can be rectangular or square.
- A matrix with only one row can exist: that's right, it is actually called a row matrix.
If you found this article useful, don't forget to share it with your colleagues and continue browsing the lessons we offer you at unProfesor.
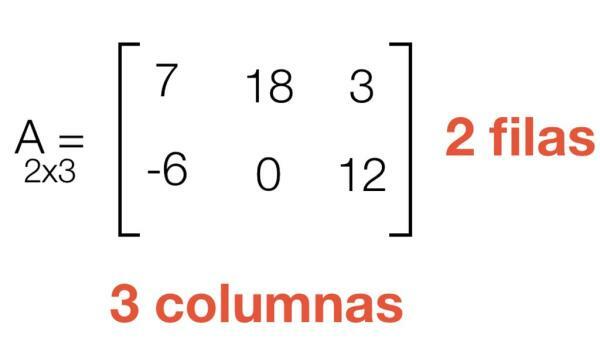
Image: Learn AI
If you want to read more articles similar to What is a matrix and examples, we recommend that you enter our category of Algebra.
Bibliography
- Ayres, F., Díez, L. G., & Vázquez, A. g. (1962). Dies (No. QA371. A918 1992.). New York: McGraw-Hill.
- Britton, J. R., Bello, I., & Campos, E. L. (1982). Contemporary Mathematics (No. 510 B7784m Ex. 1). Harla.