What is a HEXAHEDRON and its characteristics

A hexahedron is a polyhedron made up of six faces. which are polygons with five sides or less. In this new lesson from a Teacher we will study what is a hexahedron and its characteristics. To do this, we are going to review the concept of a polyhedron, and then internalize what a hexahedron is, its concept and characteristics.

A hexahedron is a polyhedron that is characterized by being made up of six faces. Those faces are polygons with five sides or fewer.

In other words, a hexahedron is a three dimensional figure which is formed by several polygons that can be triangles, quadrilaterals or even a pentagon.

We can specify that the hexahedron is a convex polyhedron because any line segment that joins any two of its points will be contained within the polyhedron.

When all the faces of the polyhedron are congruent squares, that is to say that its sides are all equal, then we speak of a regular hexahedron. These regular hexahedrons are cubes made up of six equal squares.

There are different types of hexahedrons,

with different amounts of vertices and edges, but always with six faces, since that is the main characteristic of hexahedrons. There are many types of hexahedrons but there are a few that are easy to distinguish.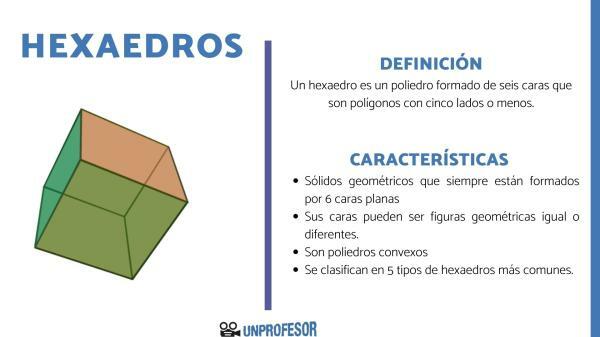

A polyhedron It is any geometric figure with three dimensions that is constituted by a finite number of faces which in turn are polygons.

Polygons are two-dimensional figures while polyhedra are three dimensional figures, therefore we can calculate not only its area and perimeter but also we can calculate its volume.

For example, a square drawn on a piece of paper is a polygon, while a box that has width and height is a polyhedron.

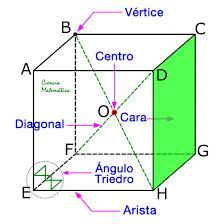
Elements of a polyhedron

Polyhedra have certain elements, and they are:

• faces: polygons that make up the sides of a polyhedron.
• edges: segments in which two faces of the figure meet.
• vertices: points where several edges meet.
• dihedral angle: angle formed by the union of two faces, and depends on the number of edges it has.
• polyhedron angle: angle formed by the sides that coincide in the same vertex, and depends on the number of vertices it has.

• Rectangular prism. Its body is formed by four quadrilaterals and whose bases are parallel rectangles. It is also known as a cuboid and obviously has six faces because it is a hexahedron. It also has four sides, eight vertices, and twelve edges. This is the best-known hexahedron, although we do not mention it by any of these names, but refer to it as a "box".
• pentagonal pyramid. Its base is a pentagon and its lateral faces are triangles. It has five faces that have three sides and one that has five. In turn, it has six vertices and ten edges. Its image differs somewhat from the most well-known Egyptian pyramids.
• Double tetrahedron. Formed by two pyramids with a triangular base, that is, it has six faces on three sides. It also has five vertices and nine edges. Being triangular based, all its faces are triangles. If all the triangles that form it are equilateral, then it is a regular tetrahedron.
• Cube. It is formed by six equal faces that are squares. Each of its faces has four vertices and four sides. It is the most common of the hexahedrons.
• Parallelepiped. It has the same number of faces and vertices as a regular cube or prism, but with the difference that one of its faces is a parallelogram. That is to say, that one of its faces will have four sides, in which each pair of opposites will be equal to each other but different from the others.

There are other types of hexahedrons apart from those just mentioned, but we cannot always associate them with a name specific or a particular figure, but are recognized from the characteristics that these possess polyhedra.

The elements of every hexahedron are:

• faces: sides of the hexahedron
• edges: union of two faces
• vertices: points at which edges meet
• dihedral angle: is formed by the union of two faces
• Polyhedron angle: It is constituted by the sides that coincide in a vertex

If you liked this lesson from a Teacher, don't forget to share it with your classmates. You can keep browsing the web to find more content like this.