6 parts of a BINOMIAL

The parts of a binomial are the terms, variables, coefficients, exponents, degree, and term. In this new lesson from a Teacher we will see what are the parts of a binomial. We will begin by reviewing the concept of polynomial and its types and then introduce ourselves to the concept of binomial. To finish we will describe the parts of a binomial.

Index

1. What are the parts of a binomial?
2. What is a polynomial?
3. What is a binomial with examples
4. Types of binomials
5. Binomials exercise with solutions

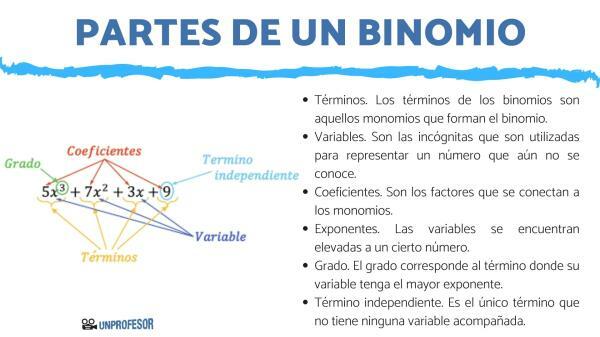
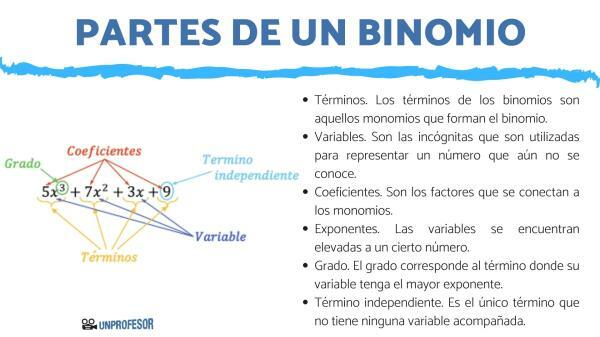
• Terms. The terms are each of the parts that make up a binomial, and that are related to each other by an addition or subtraction sign. The terms of the binomials are those monomials that form the binomial.
• variables. They are the unknowns that are used to represent a number that is not yet known.
• Coefficients. They are the factors that are connected to the monomials. They are placed next to the letter or variable that accompanies the terms.
instagram story viewer
• exponents. Variables are raised to a certain number, which corresponds to the number of times the variable should be multiplied. When the exponent is negative, the meaning is the same with the inverse operation, that is, how many times the unknown is divided by that quantity.
• Degree. The degree corresponds to the term where its variable has the largest exponent.
• Independent term. It is the only term that does not have any accompanied variable. It is only numeric. Sometimes this term may not appear.

Now that you know the parts of a binomial, we are going to better understand all the necessary terms in the world of mathematics and that will help us better understand the lesson.

When we refer to polynomials, we are talking about operations of Addition, subtraction, multiplication and division that are made up of unknowns, constants, or numbers and exponents. Polynomials can not only have more than one different variable, but also have different constants and exponents.

The terms of the polynomials are finite., and each one corresponds to an expression that has the three elements that make up the polynomials, although all three do not necessarily appear.

The only way we can solve algebraic operations with polynomials is by grouping the terms that have the same variables, otherwise it cannot be solved.

types of polynomials

To know what type of polynomial we are working with, we must know the number of terms it has.

Polynomials that are composed of a single polynomial called a monomial. When we talk about a polynomial with two polynomials or monomials, we are talking about a binomial. When a polynomial has three terms or monomials, we are talking about a trinomial. Thus continuing, we can name the polynomials.

The degree of the polynomials will be the one that corresponds to the variable with the greatest exponent.

When we refer to the word "binomial", we are talking about a word from Latin, made up of two parts. The first syllable "bi" means two, while the final part "nomos" speaks of a part of the whole according to the Greeks. A binomial is an algebraic expression that is made up of two terms.

A binomial is a polynomial that is always composed of two terms. We can also say that it is made up of two monomials and that they are related through addition or subtraction. From what we said earlier, each binomial is a polynomial formed by two monomials. To keep in mind, not all polynomials are binomials, since they can contain more terms.

To know what the degree of a polynomial is, we must look at the term that has the greatest exponent. And to add or subtract the coefficients of the binomials, we must take into account that these must be similar, otherwise we will not be able to carry out the operation.

Here we leave you a review of the different types of binomials.

square of a binomial

Also called Perfect square binomial. The sum of two y terms squared is equal to the square of the first plus twice the first times the second plus the square of the second. In a Teacher we tell you what is a squared binomial with examples.

(a+b)² = to² + 2 a b + b²

(a−b)² = to² − 2 a b + b²

Example

(x+3)² =x² + 2 x 3 + 3²

(x+4)² =x² + 2 x 4 + 4²

cube of a binomial

Also known as a perfect cube trinomial. The sum of two terms and raised to the cube, is equal to the cube of the first by triple the square of the first times the second plus triple the first times the square of the second plus the cube of the second.

(a+b)³ = to³ + 3 a² · b + 3 · a · b² +b³

(a−b)³ = to³ − 3 a² · b + 3 · a · b² -b³

Example

(x+2)³ =x³ + 3 x² 2 + 3 x 2² + 2³

(x−5)³ =x³ −3 x² 5 + 3 x 5² − 5³

Difference of squares

This type of binomial is known as difference of squares and it consists of just that. The difference of the square of two terms is equal to the difference of the two terms times the sum of the two terms.

to² -b² = (a - b) · (a + b)

Example

7² -(3x)² = (7 + 3x) · (7 − 3x)

Let's put what we've learned into practice!

Determine what type of binomial is….

1. x² + 2 x 5 + 5²
2. (2 + 4x) · (2 ​​− 4x)
3. (3x)² − 2 3x 2y + (2y)²
4. and³ − 3 y² 8 + 3 and 8² − 8³
5. (5 + 2y) · (5 − 2y)
6. x³ + 3 x² 1 + 3 x 1² + 1³

Solutions

1. (x+5)² square of a binomial
2. to² -b² Difference of squares
3. (3x − 2y)² square of a binomial
4. (y − 8)³ cube of a binomial
5. 5² − (2y)² Difference of squares
6. (x+1)³ cube of a binomial

If you liked this lesson from a Teacher, don't forget to share it with your classmates. You can continue browsing the web to find more content like this.

If you want to read more articles similar to Parts of a binomial, we recommend that you enter our category of Algebra.